標準正規分布の幾何学的対称性

標準正規分布に関する幾何学的対称性の動画紹介

1. まず、コイン投げの繰り返しゲームに手数料を考慮して繰り返すと最大獲得額は必ず27％ルール（確率点0.612）に従う説明が始まります。
2. その時の標準正規分布上に、正方形と円が同時に描ける鍵が見つかったことを紹介します。この円と正方形に加えて2種類の微分方程式で描ける曲線が登場します。
3. それらに古代エジプト作画法と三平方の定理を用いた提案を行います。
4. さらに、回転対称性や個性ある図形との幾何学的特徴やその調和を紹介しています。

https://www.research.oit.ac.jp/oitid/archive/2020/wp-content/uploads/2020/09/oit2020-09-03-06-from-shotcut.mp4

ウォーミングアップ　＆　狙い！

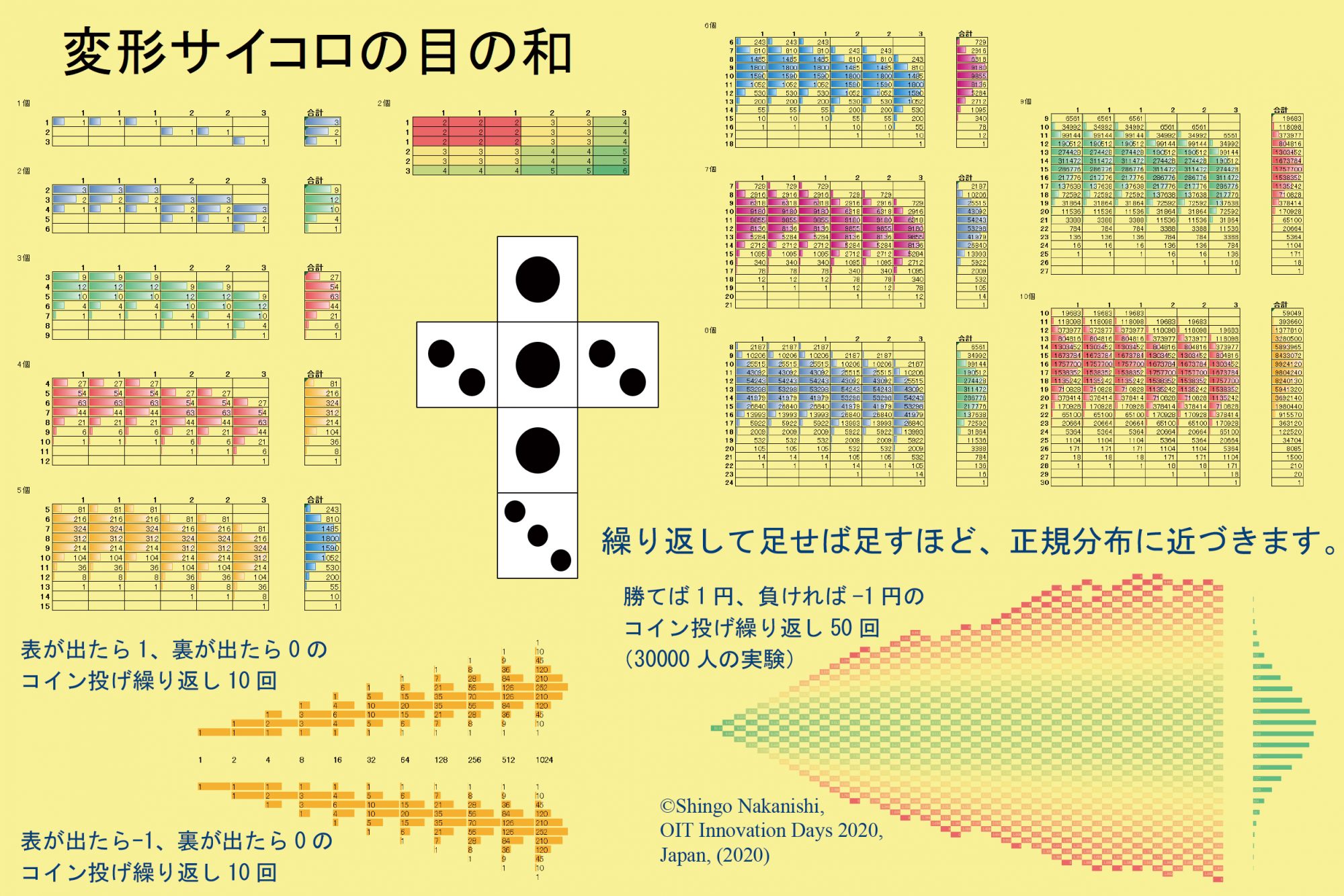
• 右図のような変形サイコロの目を繰り返し足していくと、正規分布に近づくことが知られています。
• 同様に、勝てば1円を得て、負ければ1円を支払う繰り返しコイン投げを考えます。30,000人分の50回連続試行のコイン投げをゲームとして見た場合には、勝敗による損益もまた正規分布に近づくことがわかります。

一方で、計って比べて統治する文化として誕生する統計学を支援するために、古代バビロニアの頃から三平方の定理の鍵となる数値が文明とともに知られていました。

 

本研究では、この特別な正規分布と三平方の定理に注視し、先人の知恵や文化を借りながら視覚的な幾何学的特徴の解明を狙っています。

27パーセントルール（片側確率点0.612003）だった！

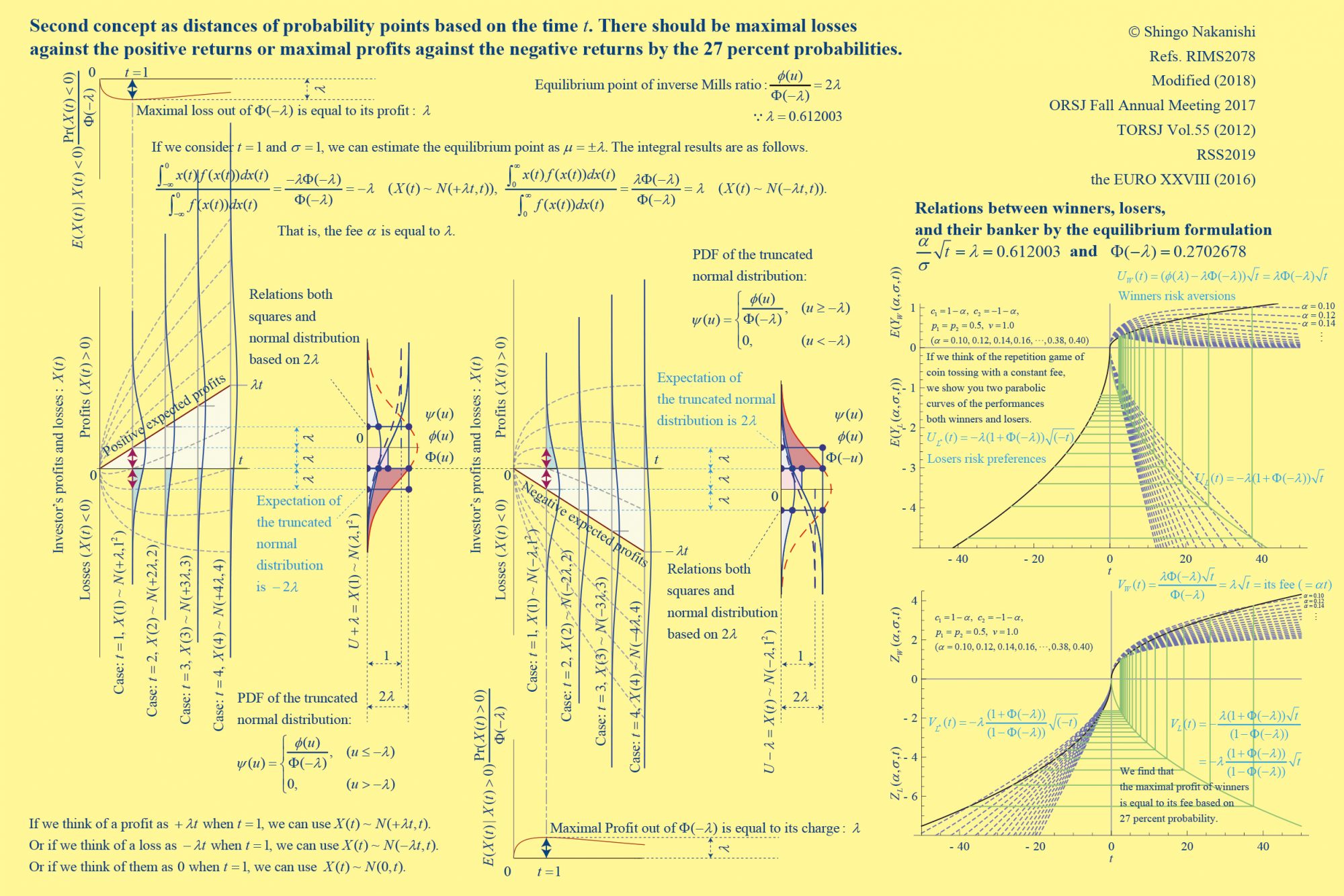
勝者が手数料を支払ってでも稼ぐ最大獲得賞金額を計算すると確率点が0.612になります。

この数値は、約100年前に英国のカール・ピアソンによって見つけられています。その後、英国のコックスが正規分布のクラスタリングを提案し、米国のケリーが27％ルールとして研究しています。研究責任者も、独自の方法でこの数値に辿り着きました。この確率点0.612は、正規分布の幾何学的解明に大変重要な役割を果たします。

• 左図の左側図は、そのときの手数料と最大獲得賞金が釣り合っている場合です。
• 左図の右側図は、その傾向が放物線になり、手数料を考慮した勝者獲得賞金と敗者の損失の鏡映効果として図示しています。

正方形、円形、二組の微分方程式による曲線へ！

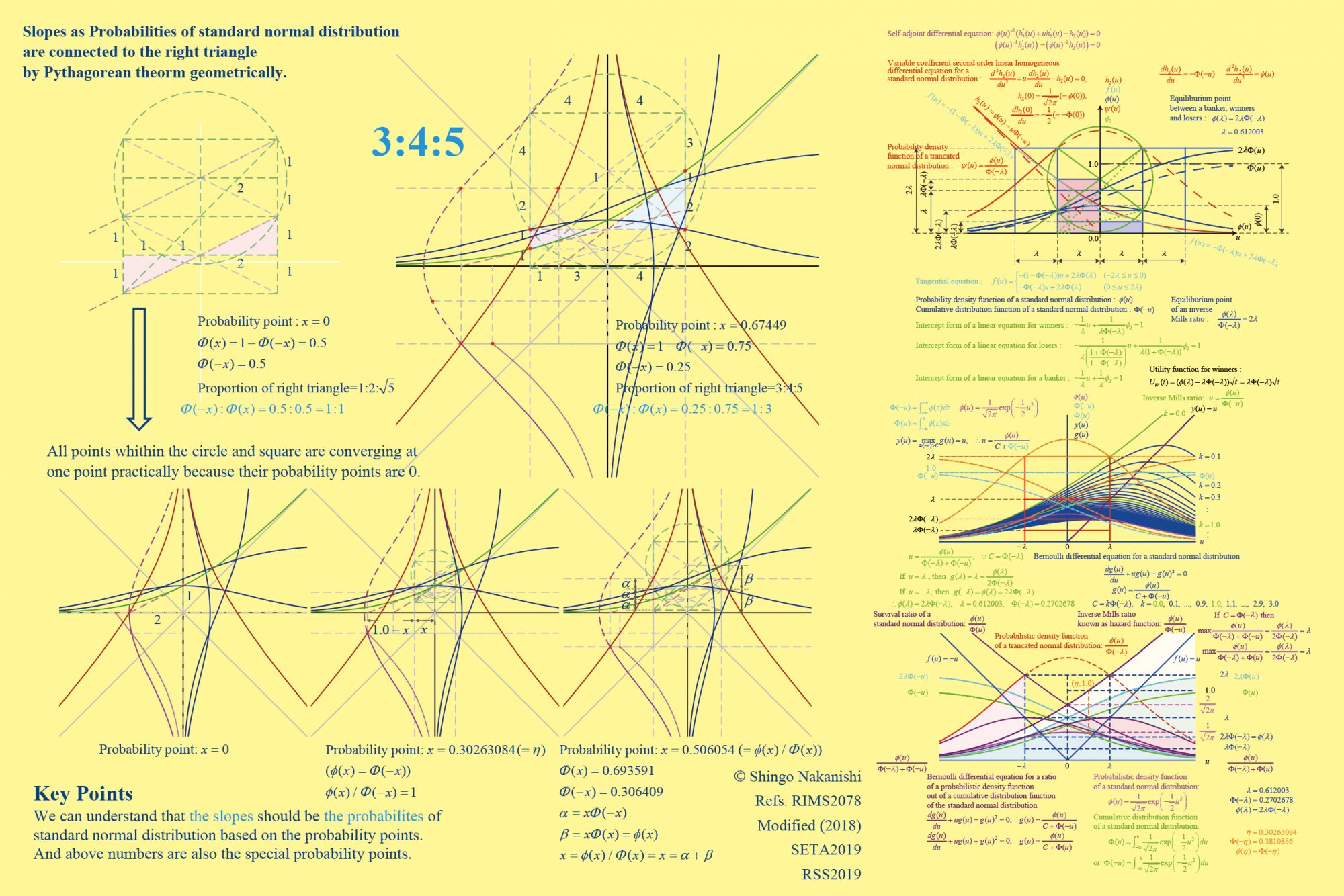
• アスペクト比（縦横比）を1にとり、確率点0.612を2倍して考察すると標準正規分布に正方形を描けます。
• そこに、勝者が最大賞金を得る確率は27％になるので、全体の勝者獲得賞金額を27％で割り、勝者一人当たりとして見積もる場合と比較します。すると、円を描く鍵が得られます。
• その後に、累積分布の積分形を意味する微分方程式と逆ミルズ比を意味するベルヌーイ型の微分方程式が見つかり、同時にこれらを図示できました。
• さらに、この二組の微分方程式と標準正規分布の幾何学的特徴を調べるために、奥行きを感じさせない古代エジプトの作画法を適用します。その結果、25％、50％、75％等、どの確率でも三平方の定理により描けることを発見しました。

直角三角形と原点の重要性とその対称性がわかった！

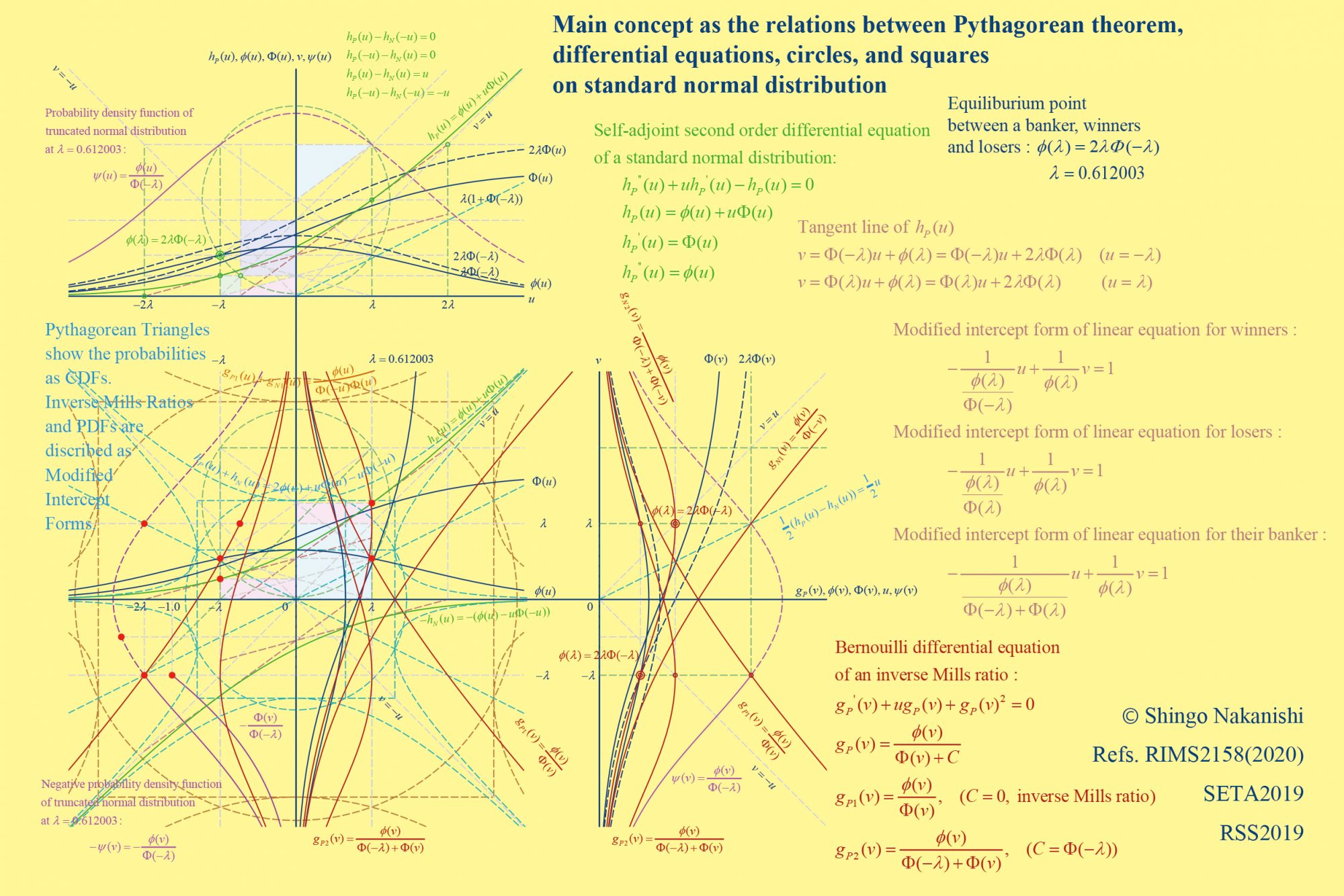
 実は、上図では、片側確率点が0のときが大変重要でした。

では、右図のように原点を中心に第4事象まで図のイメージを拡大させながら、原点を中心に円を描きます。すると、二組の累積確率の意味がより鮮明になります。

加えて、右図には、切片系の方程式の修正版を図示しています。

ここで、対称な二組の二階線形微分方程式、二組のベルヌーイ型微分方程式を右図の表示のように考えます。すなわち、媒介変数表示形式、もしくはパラメトリック方程式として表示し、確率の比による重ね合わせを実践します。すると、

1. 確率の比による和の表示形式では回転による対称性
2. 確率の比による差の表示形式ではせん断による対称性

を表示できます。詳しくはこのリンク（アニメーション）をご確認ください。

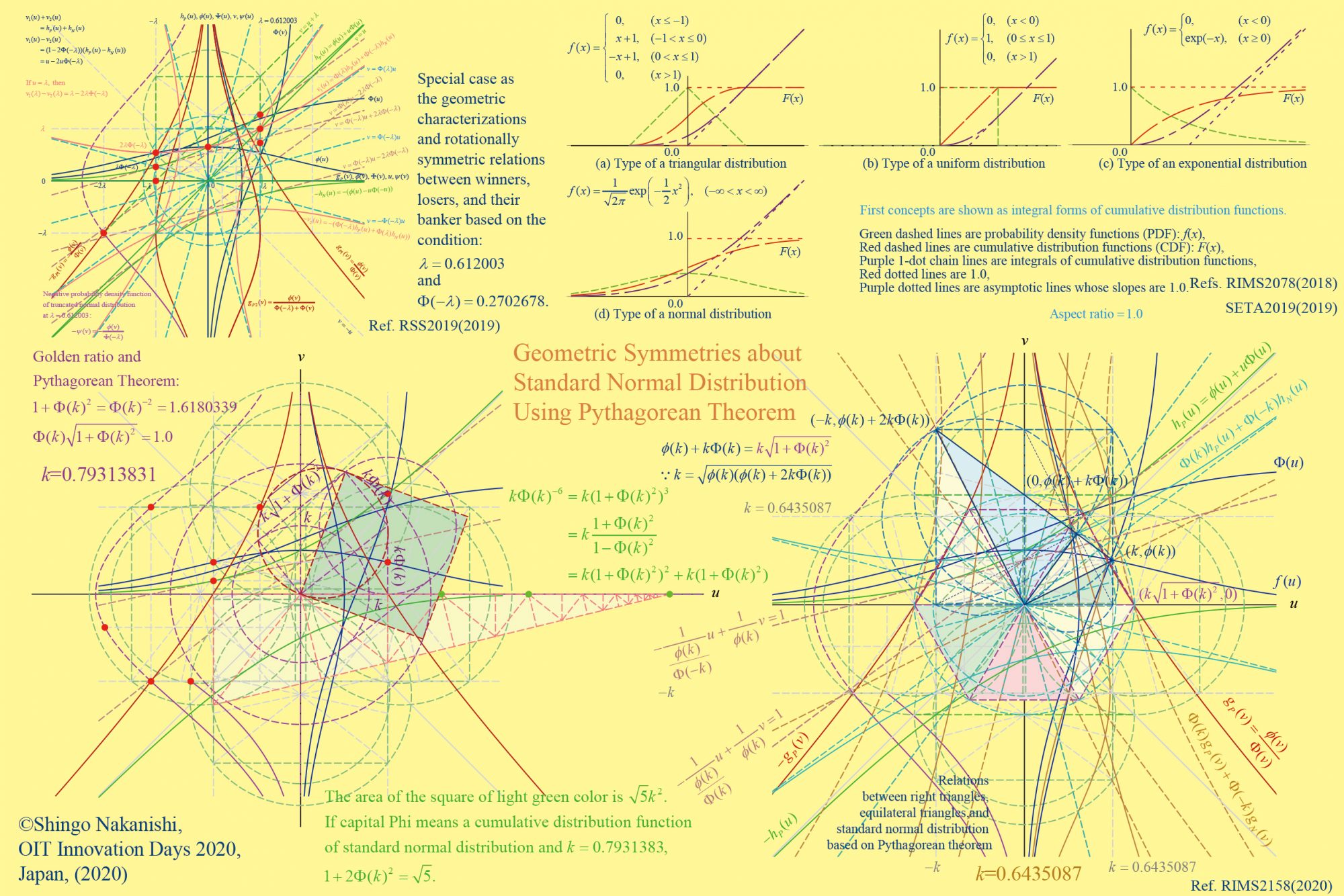
円積問題、正三角形や黄金比とも相性が良かった！

さらに、応用例として、

• 回転対称性から、正三角形や黄金比等と相性が良かった確率点を左図に示しています。
• また、逆に図示していませんが、円と正方形を固定して正規分布を変形させていくと、円積問題とも整合性が良いことがわかっています。

以上の成果を求めて、左図の上側の図に示す確率点0.612の幾何学的特徴の解明から研究を継続しました。多くの失敗を繰り返し、先人の知恵や歴史や文化にも頼りながら提案してきました。その結果、得られた成果は神様の設計図を感じる程美しい幾何学模様が描けました。また、本学の先生方をはじめ多くの方々からも助言・支援を受けたことを付記して感謝し、独自の発想で標準正規分布に円、正方形、微分方程式による曲線を描き重ねながら三平方の定理による累積確率評価という構想に辿り着きました。

では、結果までのアプローチ方法は一体何？それがこの研究の独自性？

研究責任者は数学者やデザイナーではございません。膨大なデータ処理やその数式処理や検証には、Excel、Mathematicaが不可欠でした。また、図のイメージ化や創作活動には、歴史、先人・専門家の助言、分野外の文献に加え、Illustrator、zoomIt等でのスケッチと供に協働作業アプリやITツールを多数活用しました。研究者や現場でお困りの方、皆様の取り組みのヒントやプロトタイプになれば幸いです。

上記の本研究の関連作品にご関心のある方は、情報センターの中西真悟のHPへどうぞ！