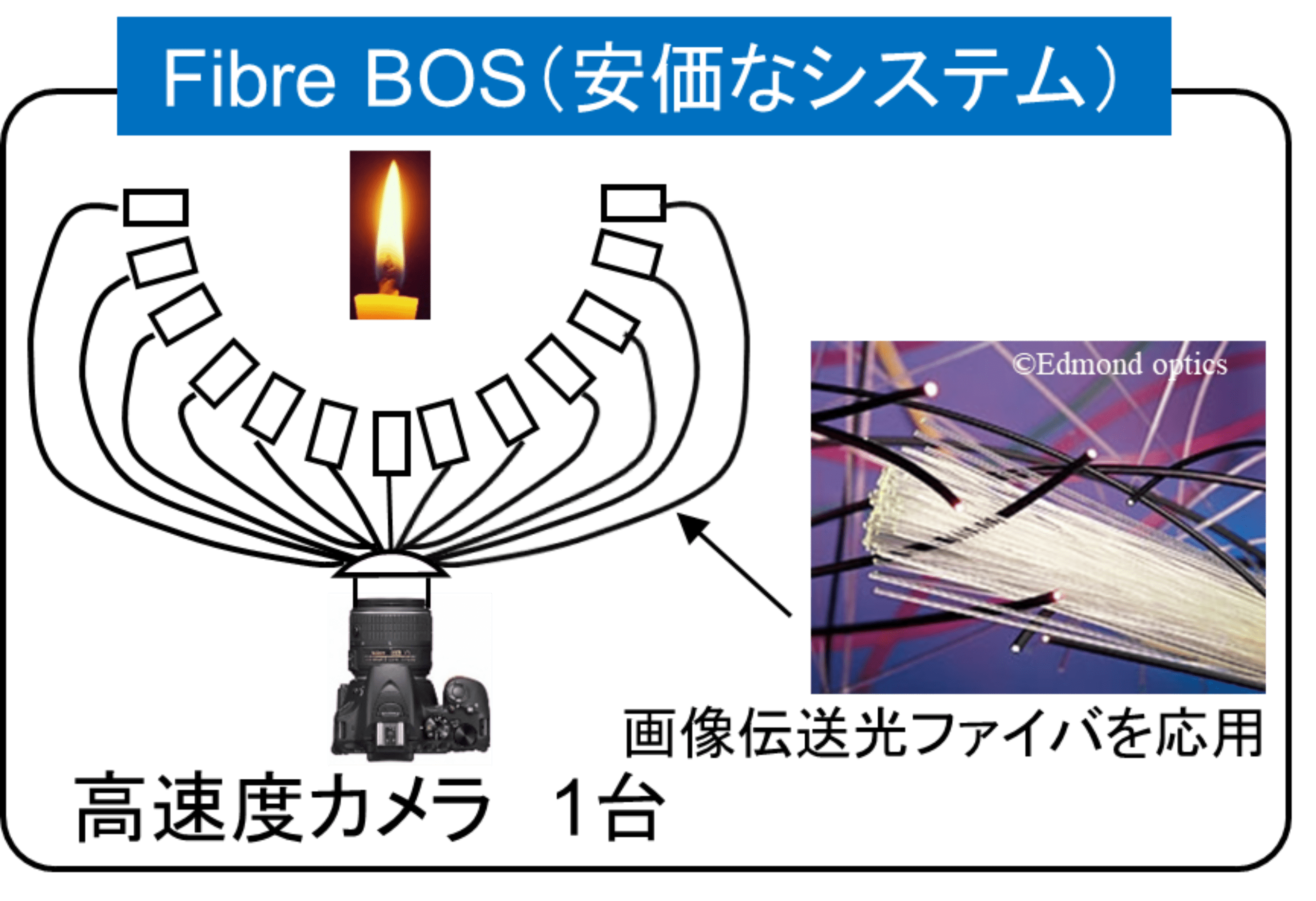
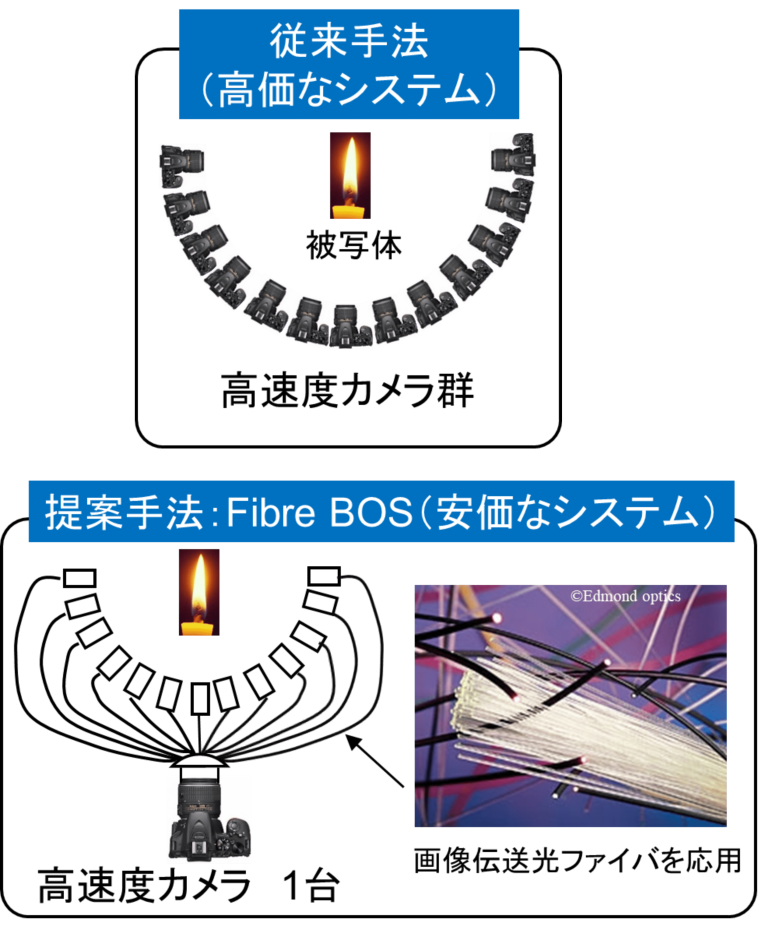
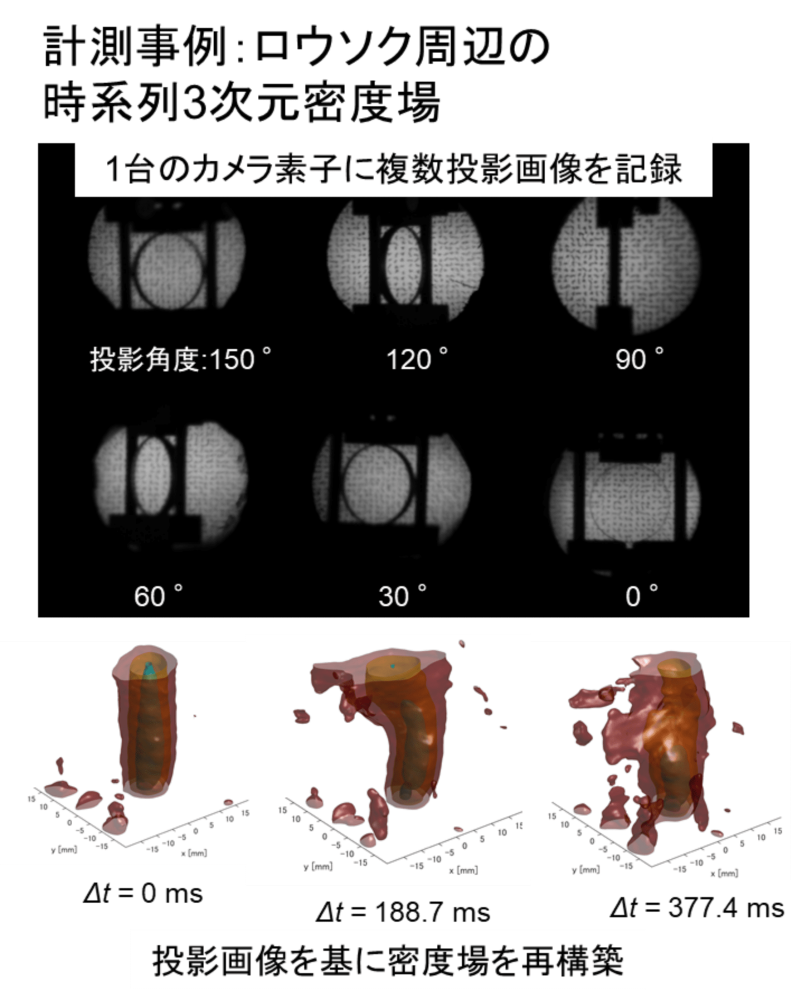
1台の高速度カメラで3次元密度場の時系列計測が可能な新たな可視化手法を開発しました．従来法と比較して1/10のコストで複雑流動が評価できます．航空機・自動車・流体機械・家電の周辺に生じる熱の移流などの流体現象の把握に役立ちます．
3次元密度場計測には，複数方向からの投影画像の撮影が必要です．従来法では高価な高速度カメラを十数台使用しておりました．本計測法は，高価な高速度カメラの代わりに画像伝送光ファイバーを用いて，1台の高速度カメラで3次元密度場計測を達成できます．
物体周辺の密度場を計測するために，熱電対や浮揚した粒子を必要としません．これにより，流れを乱すことなく密度場計測が可能です．特に，低コストで4次元時空間の密度場計測が可能です．測定対象の大きさと形状に制約がございますので，ご気軽にご相談ください．
論文
「The principle and characteristics of an image fibre Background Oriented Schlieren (Fibre BOS) technique for time-resolved three-dimensional unsteady density measurements」(2021)『Experiment in Fluids』60:170
「Flexibility and versatility enhancements due to a portable optical system for the Background-Oriented Schlieren techniques」(20231)『Journal of Visualization』26p.551–561.
研究シーズ・教員に対しての問合せや相談事項はこちら
技術相談申込フォーム© INNOVATION DAYS 2025 智と技術の見本市.
