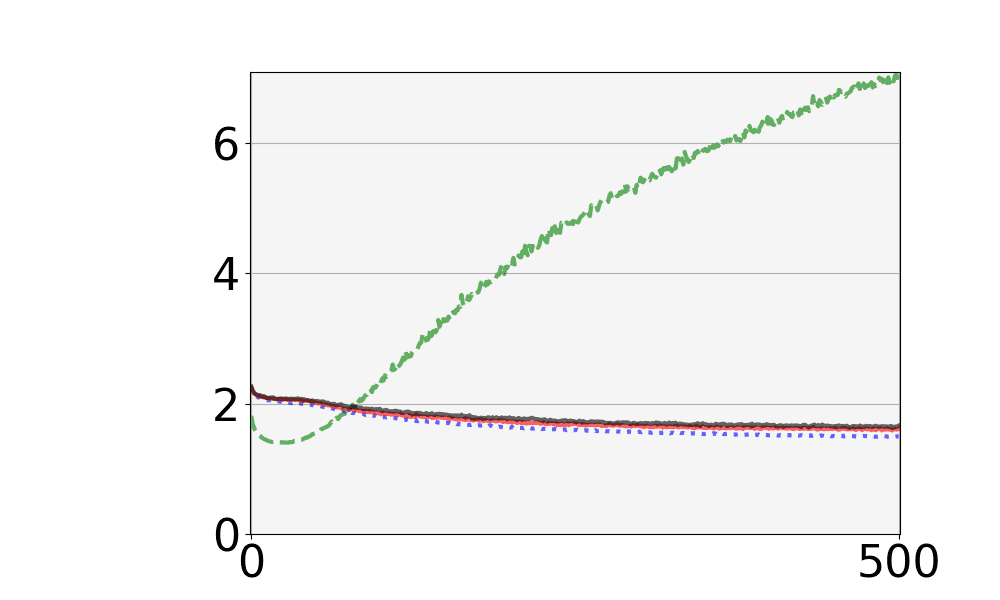
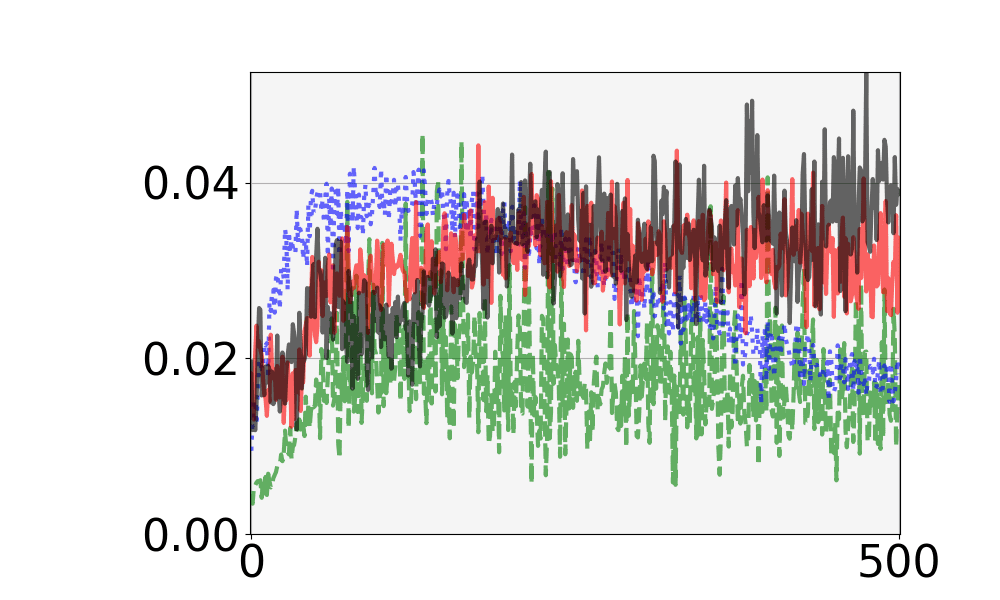
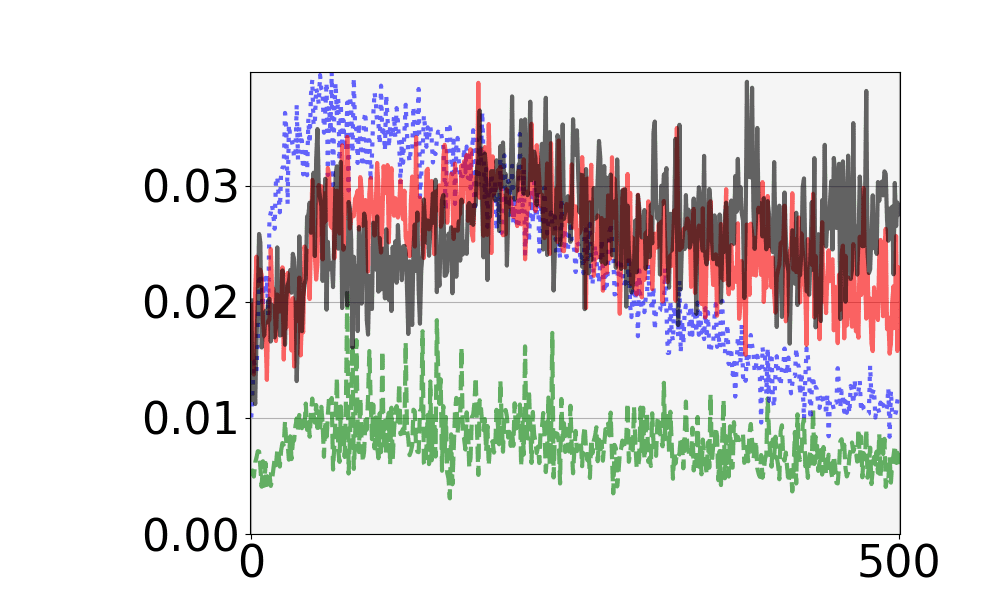
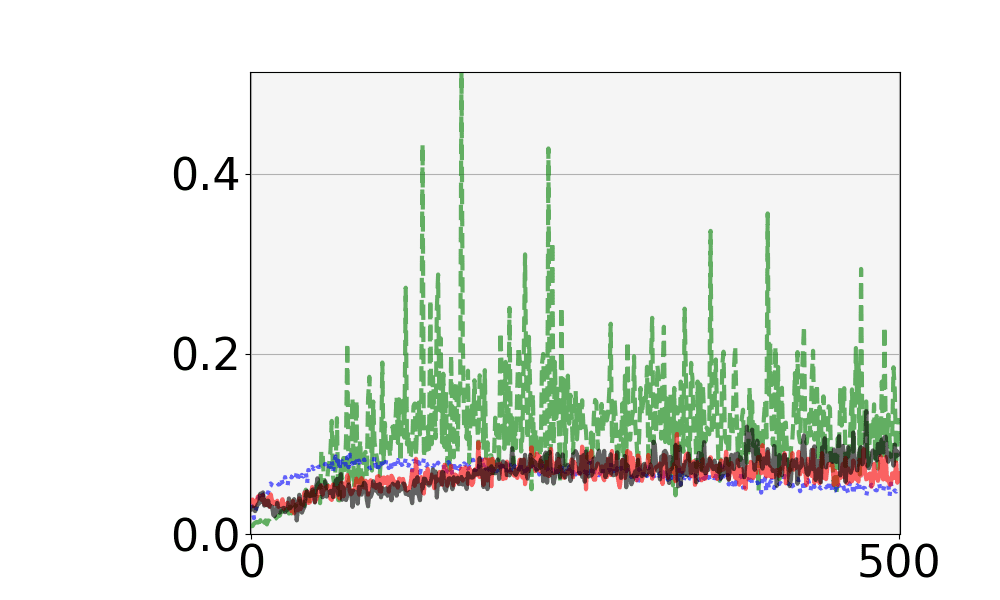
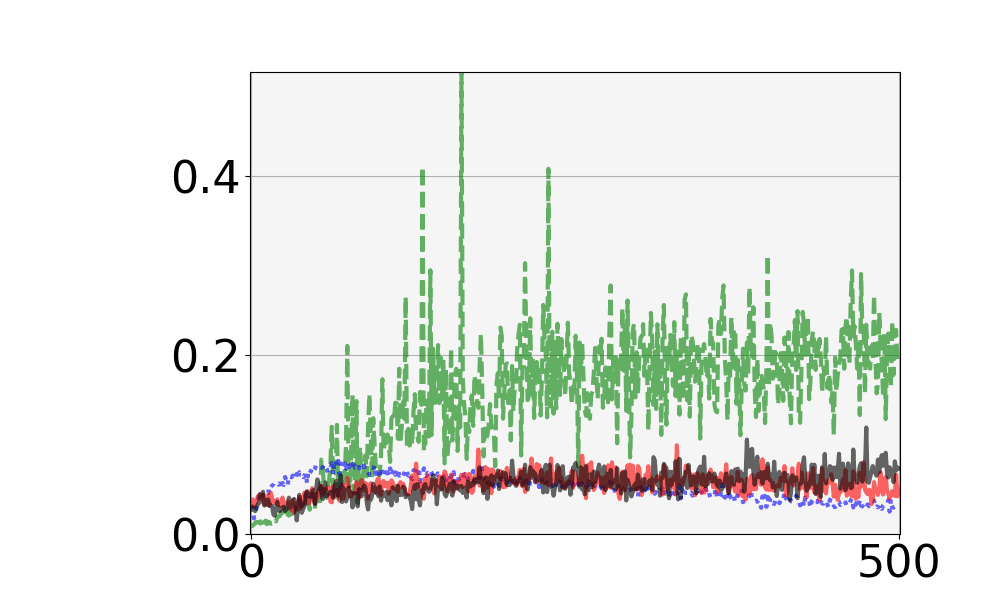
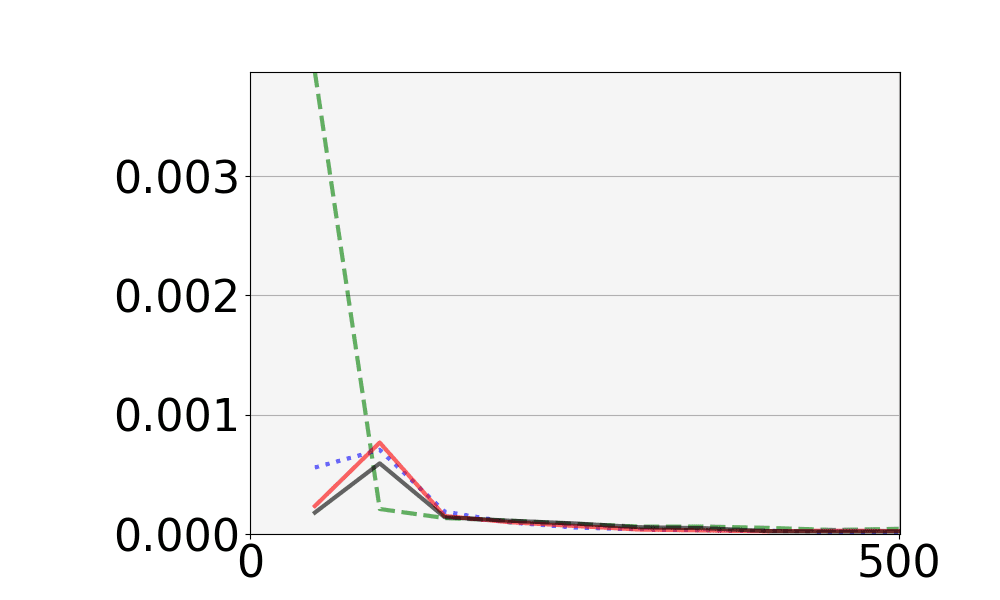
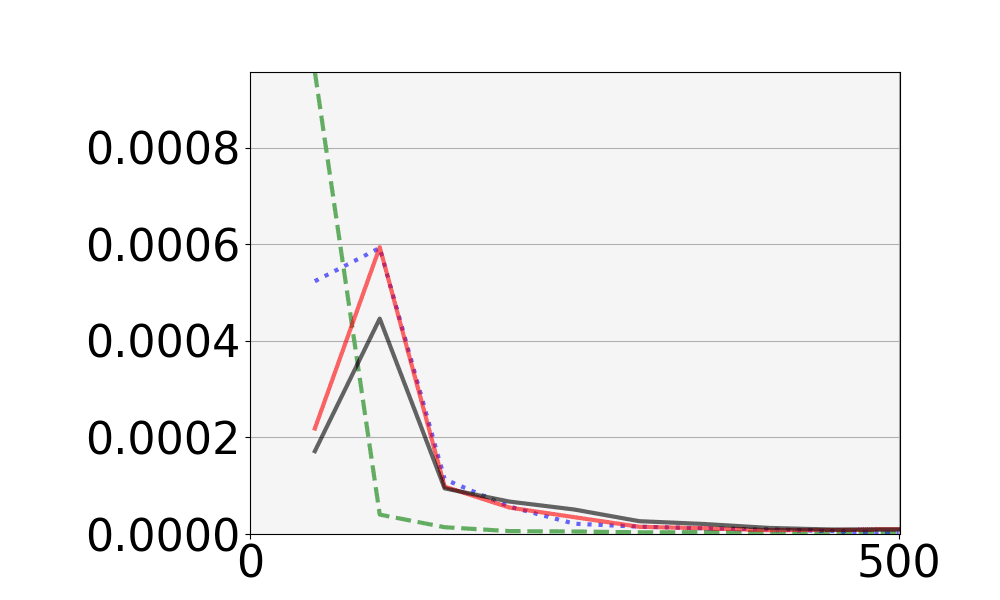
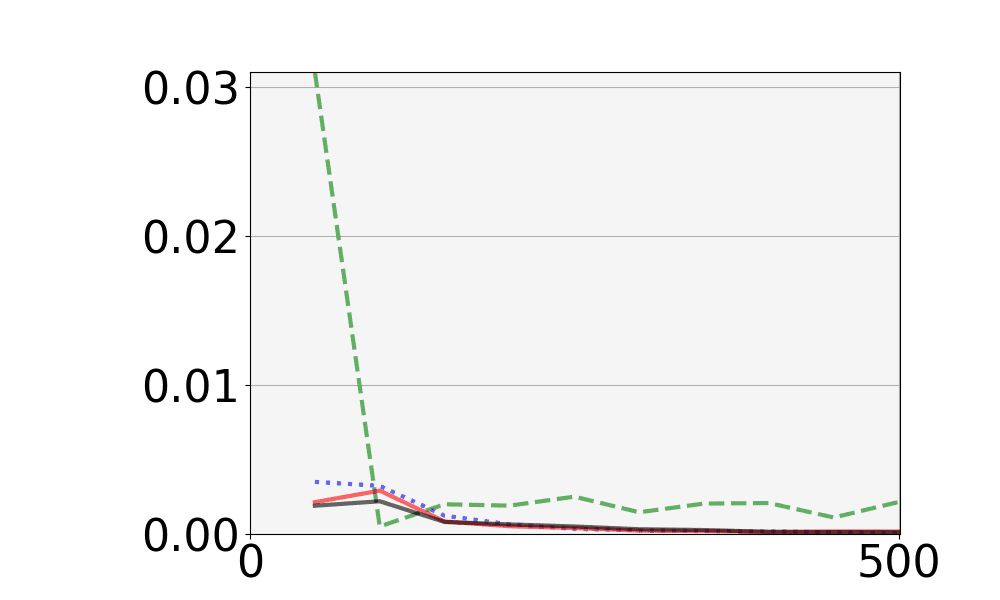
本研究で使用した組合せデザインであるドロップアウトデザインの定義と具体例を述べる.
定義.
\(V_1,V_2,\ldots,V_n\) をそれぞれ要素数 \(v_1,v_2, \ldots,v_n\) の異なる点集合とし, ブロック集合 \(\mathcal{B}\) を
\[
\mathcal{B} = \{ \{B_1 | B_2 | \cdots | B_n \} | \ B_i \subset V_i, B_i \neq \emptyset,\ 1\le i \le n \}
\]
とする. 各\(B_i\)をサブブロックと呼ぶ. \(\mathcal{B}\)のうち, 連続する\(t\) 個の点集合におけるサブブロックの集合を
\[
\mathcal{B}|_{V_{i}V_{i+1}\cdots V_{i+t-1}} = \{ \{B_i | B_{i+1} | \cdots | B_{i+t-1}\} | \ B_j\subset V_j \},\ i=1,\ldots,n-t+1
\]
とする. このとき, 次の二つの条件を満たす\( (V_1,V_2, \ldots,V_n ; \mathcal{B})\)を\((d_1,d_2, \ldots,d_t)\)型 ドロップアウトデザインという.
(i) \(1 \leq i \leq n-t+1\) について, 各\(V_j, i \leq j \leq i+t-1\), の任意の\(d_j\) 個の点を同時に含むブロックが\(\mathcal{B}|_{V_{i}V_{i+1} \cdots V_{i+t-1}}\)の中にちょうど\(\lambda^{(i)}\)個存在する
(ii) 各 \(0 \le g_j \le d_j,\ i\le j \le i+t-1, \ g_i+g_{i+1}+\cdots + g_{i+t-1}\ge 1\), に対して,各\(V_j\)の中の任意の\(g_j\)個の点を含む \(\mathcal{B}|_{V_{i}V_{i+1}\cdots V_{i+t-1}}\)中のブロックの数は選択する点に依存しない.
例.
点集合をそれぞれ \(V_1=\{0,1,2,3\}, V_2=\{ {\it 0,1,2,3}\}, V_3=\{ {\bf 0,1,2,3,4,5}\}\) とする.
以下のブロック集合は\((2,1)\)型 ドロップアウトデザインをなし, 会合数\(\lambda_{2,1}^{(1)} = \lambda_{2,1}^{(2)} = 1\)を持つ. 任意の3点 \(x,y \in V_1, {\it z} \in V_2\) また \({\it x,y}\in V_2,\ {\bf z} \in V_3\)はちょうど1つのブロックに含まれることが確認できる.
\[
\begin{array}{llll}
\{0,1\ |\ \it{1,2}\ |\ \bf{0,1,2}\}, &
\{2,3\ |\ \it{1,2}\ |\ \bf{3,4,5}\}, &
\{1,3\ |\ \it{1,3}\ |\ \bf{1,2,5}\}, &
\{0,2\ |\ \it{1,3}\ |\ \bf{0,3,4}\}, \\
\{1,2\ |\ \it{0,1}\ |\ \bf{1,2,4}\}, &
\{0,3\ |\ \it{0,1}\ |\ \bf{0,3,5}\}, &
\{1,2\ |\ \it{2,3}\ |\ \bf{0,2,3}\}, &
\{0,3\ |\ \it{2,3}\ |\ \bf{1,4,5}\}, \\
\{1,3\ |\ \it{0,2}\ |\ \bf{0,4,5}\}, &
\{0,2\ |\ \it{0,2}\ |\ \bf{1,2,3}\}, &
\{0,1\ |\ \it{0,3}\ |\ \bf{0,1,3}\}, &
\{2,3\ |\ \it{0,3}\ |\ \bf{2,4,5}\}.
\end{array}
\]
ドロップアウトデザインの主な構成法として直交配列や有限幾何を用いた構成法が知られている [1, 2]. また, ここでは, 深層学習やドロップアウト法についての詳細は省略する.
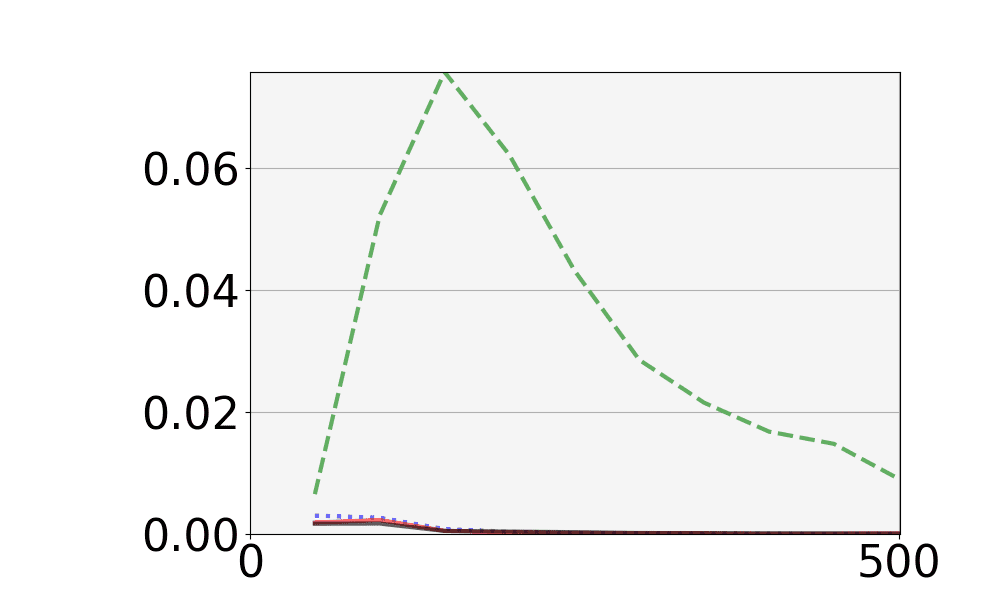
本実験は, 有限アフィン幾何を用いて構成される(1,2)型かつ(2,1)型ドロップアウトデザインを用いて実施した. この構成法から生成されるデザインによるモデルは, 素数ベキ \(q\), 整数 \(t\), \(d \leq 3\) について, 層数 \(q^{d-t}\), 各層のノード数 \(q^t\), ドロップアウト率は \(1 – 1/q\) をもつ.
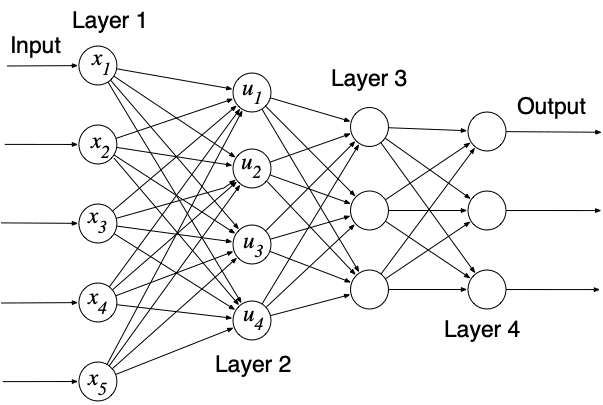
ドロップアウトデザインの点集合をネットワークにおけるノードの集合に対応させ, ブロックを一つのミニバッチで学習する部分ネットワークとする. 各ノードに番号付を仮定し, サブブロックで活性化するノードを指定する. 1エポックで各ブロックを一度ずつ重みの更新に使用する. また, エポック終了時にブロックの順序を巡回させるブロックシフトと, 順序を固定したまま使用する2通りの方法を実施した.