NUMBERS 天才数学者の事件ファイル

非常に面白いアメリカドラマです。

主人公の天才数学者チャールズ・エプスが兄のFBI特別捜査官ドン・エプスを数学で、事件解決に協力して、次々と難事件を解決していくドラマです。

事件が起こっていますので、そこには多くのデータが存在しており、そのデータから確率論に従って、捜査を行い事件解決に向かう訳ですから、色々な場面で確率論に基づく数理モデルが登場します。

マルコフ過程

次に起こる事象の確率が、現在の状態に至るまでの経過とは関係なく、現在の状態によってのみ決定される確率過程の事です。

交通渋滞予想や天気予報等が、だいたいマルコフ過程に相当するのではと思います。

例えば夏季において、雨の日の翌日の天気が晴れである確率が４０%であるとします。

その場合、もし本日の天気が雨の場合、翌日の天気が晴れになる確率は、前日までの天気の状態に関わらず４０%となります。

マルコフ過程を数式で表すと次式の通りとなります。

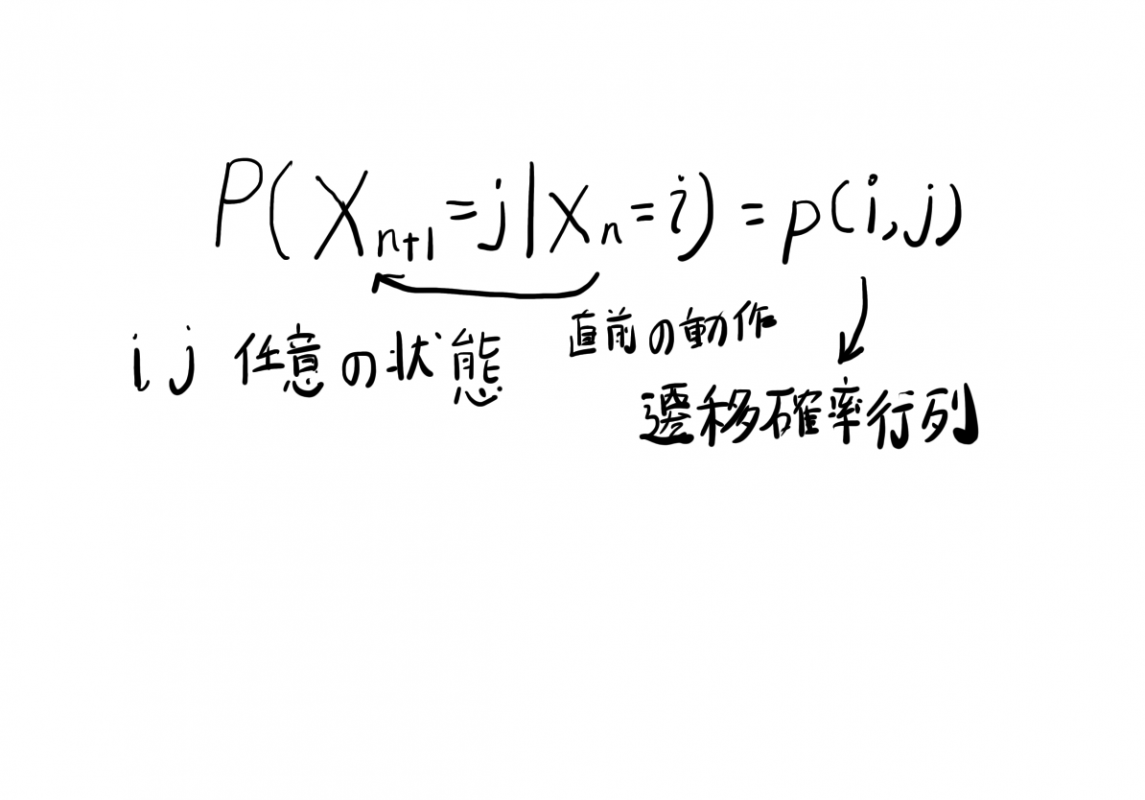
NUMBERS 天才数学者の事件ファイルでは、囚人が、護送される時に、外部協力者と陰謀して、マルコフ過程に基づき、護送車が転倒事故を起こす確率を高めて、事故に見せかけて脱走するというシーンがありました。

これはドラマ上の悪い事例ですが、現実生活においても、何かを成功に結び付けようと考える場合、可能な限り、外部要因を除き、シンプルな確率モデルに結び付けるという思考方法が重要であると考えます。

確率論と数理モデル

以上のように犯罪捜査のドラマを事例にあげましたが、確率論と数理モデルは密接な関係にあります。

世の中のあらゆる現象や行動には確率論で溢れています。

このような確率論と数理モデルにご興味ある方はぜひ大阪工業大学　情報科学部　データサイエンス学科にご注目下さい。

大阪工業大学

研究支援・社会連携センター

シニアＵＲＡ

北垣和彦