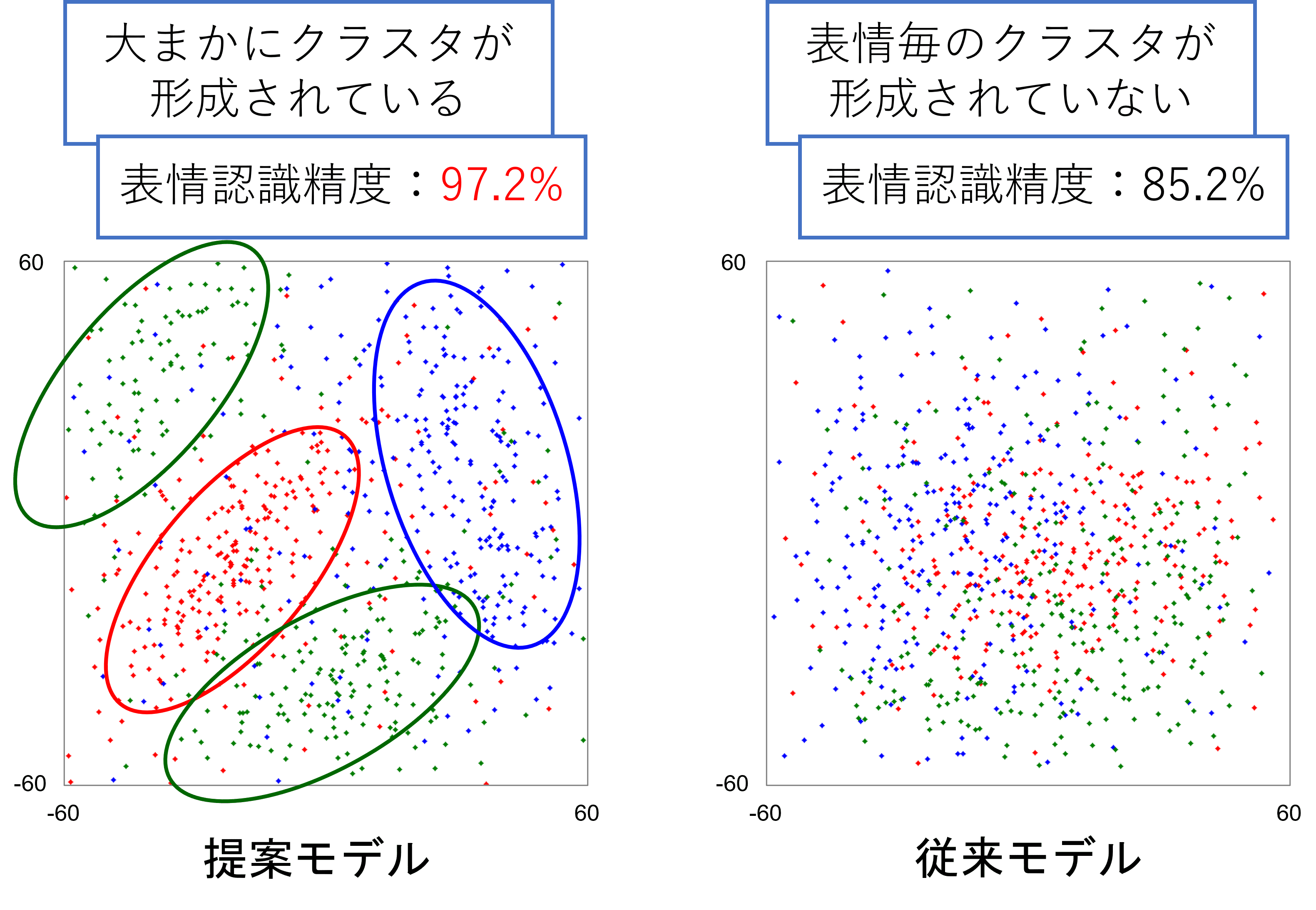
深層学習は精度の高い処理を実現できるものの，判断根拠の理解が困難になりがちである．判断根拠が理解できないままでは実応用上問題が発生するケースも多い．例えば医用データ解析など，答えを誤った際の被害が甚大となる分野では現在でもこのような手法の全面利用が法律上規制されている．これに対し，本研究では潜在変数空間のdisentanglement化手法を応用して，目的とするタスクに関係の無い特徴を排除することで，判断根拠の理解が容易な潜在変数空間の獲得を実現した． 本報告では実応用を想定した課題として，撮影環境の大きく異なる顔画像における表情認識などを扱う．この課題では被験者情報以外にも照明や化粧など，表情認識に関係の無い様々なバリエーションを持つデータベースを構築し，学習に際して表情認識に不要な特徴を取り除く手法を開発した．本手法を応用することで，表情認識精度と判断根拠可読性の向上を実現した．