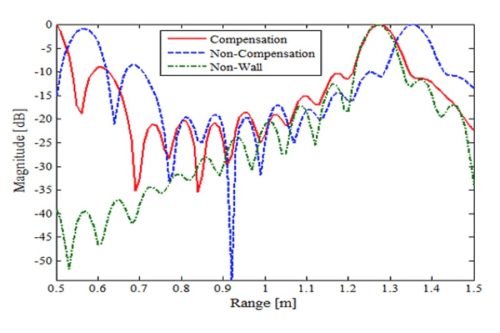
地球上の殆どの物体を占める誘電体の誘電率情報はあらゆる分野での基本量です。通常は伝送線路内に小試料を充填し、その前後の変化から誘電率を算出します。問題は木などの空間内に誘電体が分布している場合、どう計測するかです。これに対し、レーダ画像位置の変位と物体の誘電率の関係に着目した新しい計測法を考案しました。壁などの均一に材料が配分されている場合(図2)は材料の誘電率分だけ、空間内に分布している場合(図3)は等価的な誘電率分の位置が変位します。誘電率(水分)と森林バイオマスの相関より、地球規模の環境計測にも応用性があります。
論文
(2013)『2013 International Symposium on Electromagnetic Theory (URSI Commission B EMTS 2013)』p.4.
(2012)『International Symposium on Antennas and Propagation (ISAP2012)』P-32p.4.
(2012)『International Conference on Space, Aeronautical and Navigational Electronics 2012 (ICSANE2012)』SANE2012-64p.6.
研究シーズ・教員に対しての問合せや相談事項はこちら
技術相談申込フォーム
