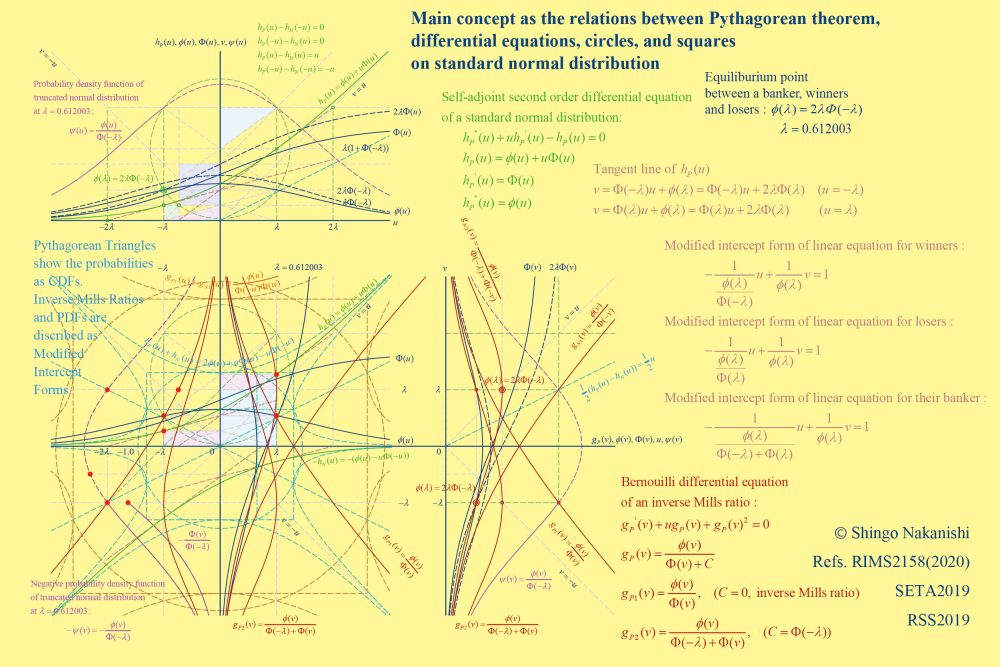
標準正規分布の幾何学的対称性
三平方の定理による累積確率評価
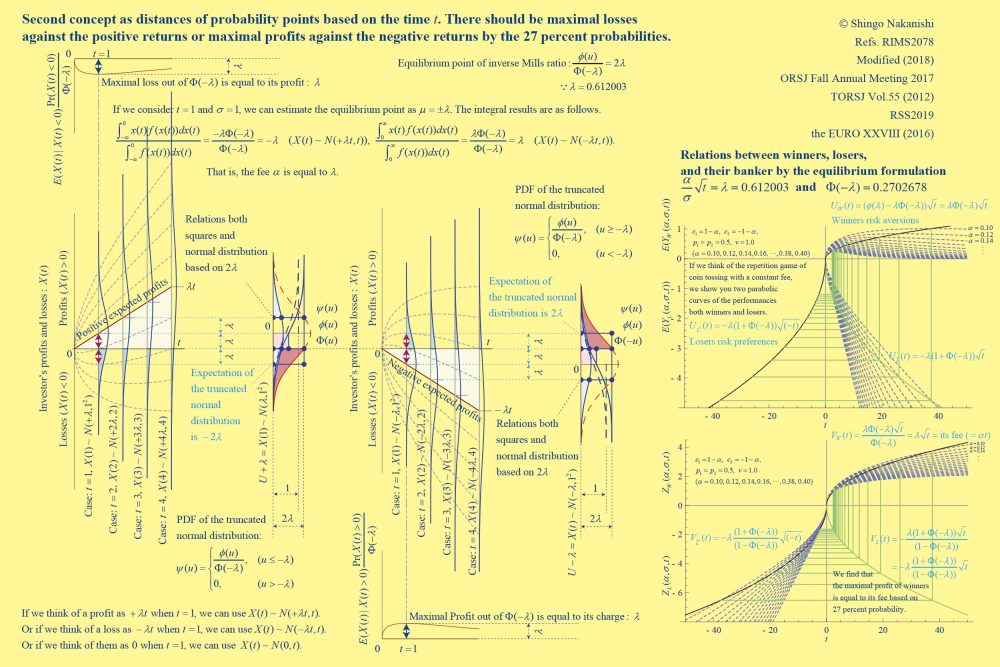
連続な確率変数の確率密度関数の積分形は、0から1までで評価できる累積分布関数です。では、累積分布関数を積分するとき、積分形の関数の一階の導関数は、累積確率として0から1までの傾きになります。つまり、直角三角形を用いた三平方の定理による評価が可能になります。そこで、標準正規分布の幾何学的対称性を応用しながら三平方の定理を用いてみると、新たな確率評価基準が思考できます。
論文
「Rotationally Symmetric Relations of Standard Normal Distribution Using Right Triangles, Circles, and Squares – Ordinary Differential Equations, Pythagorean Theorem, Equilateral Triangles, and Golden Ratio –」(2020)中西真悟『京都大学数理解析研究所講究録』(2158)p.171-183.
「Geometric Characterizations of Standard Normal Distribution - Two Types of Differential Equations, Relationships with Square and Circle, and Their Similar Characterizations -」(2018)中西真悟『京都大学数理解析研究所講究録』(2078)p.58-64.
「手数料を考慮したコイン投げの繰返しゲームの賭けにおけるすべての勝者の獲得賞金の総和最大化とその試行回数の関係」(2012)中西真悟『日本オペレーションズ・リサーチ学会和文論文誌』55p.1-26.