SDGsの分類
研究テーマ
IT・IoT・AI・ロボティクス
学科の分類
工学部電子情報システム工学科

レーダ画像からレーダ断面積とアンテナパターンが評価できる?! 近傍電磁界遠方変換理論の研究

工学部

電子情報システム工学科

波動情報システム研究室

小林弘一 教授

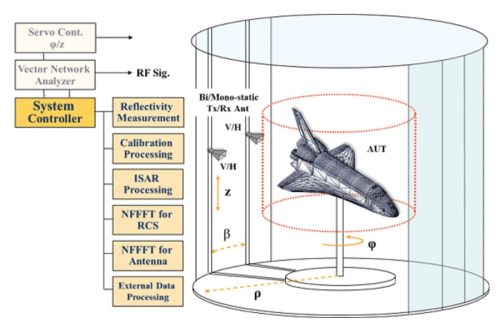
電気長の非常に大きな物体のレーダ断面積、アンテナパターンの計測は困難を極めます。このため、物体近傍の散乱電磁界を計測し、逆合成開口による画像処理後、遠方電磁界を数学的に評価する方法を確立、提案しています。

論文

「RCS Near-field to Farfield Transformation Estimation by Using GTD Target Models」(2018)KobayashiHirokazu『International Conference on Space, Aeronautical and Navigational Electronics 2018 (ICSANE2018)』SANE2018-77p.6.

「遠近傍界遠方変換における多重反射の影響について」(2019)小林弘一『電 子情報通信学会技術研究報告(宇宙· 航行エレクトロニクス)』SANE2018-90p.6.

「近傍界遠方変換によるRCS およびアンテナパターンの計測」(2018)小林弘一『電子情報通信学会技術研究 報告(宇宙· 航行エレクトロニクス)』118(135), SANE2018-25p.6.

研究者INFO: 工学部 電子情報システム工学科 波動情報システム研究室 小林弘一 教授

研究シーズ・教員に対しての問合せや相談事項はこちら

技術相談申込フォーム