一般的に実験計画法において，品種の効果の推定量の分散は任意の2つの効果の会合数が一定であるとき，等分散になりかつ最小になる.統計モデルでは推定すべき品種の効果は単純な集合として表現する.しかし深層学習では 2 部グラフの辺に推定すべき重みが対応しているため，辺集合を品種の集合と考え，その会合数をバランスさせることを考える.

完全二部グラフ\(K_{v_{1},v_{2}}\)の2つの頂点集合を\(V_1,V_2\)とし，以下の5つの条件を満たす部分グラフの集合\(\mathbf{B}=\{B_1,B_2,\ldots, B_N \}\)を考える.

[SBBDの条件]

(1) \(\mathbf{B}\)のどの部分グラフ\(B_i\)も\(V_1,V_2\)の点をすべて含む（全域条件）.
(2) \(\mathbf{B}\)の中に\(K_{v_1,v_2}\)のすべての辺はちょうど\(\mu\)回ずつ現れる.
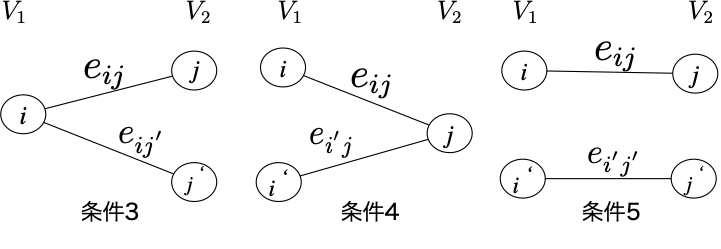
(3) 任意の2つの辺 \(e_{ij}, e_{ij’}\), \(i \in V_1\), \(j, j’ \in V_2, (j \ne j’)\) が同時に含まれる部分グラフは\(\mathbf{B}\)内に必ず\(\lambda_{12}\)個存在する.
(4) 任意の2つの辺 \(e_{ij}, e_{i’j},\ i, i’ \in V_1, (i \ne i’), \ j \in V_2\) 同時に含まれる部分グラフは\(\mathbf{B}\)内に必ず\(\lambda_{21}\)個存在する.
(5) 任意の2つの辺 \(e_{ij}, \ e_{i’j’}, \ i, i’ \in V_1, (i \ne i’),\  \, j, j’\in V_2, (j \ne j’)\)が同時に含まれる部分グラフは\(\mathbf{B}\)内に必ず\(\lambda_{22}\)個存在する.
これらの条件を満たす\(K_{v_1,v_2}\)の部分グラフの集合\(\mathbf{B}=\{B_1,B_2,\ldots, B_N \}\)をとし，\((K_{v_1,v_2} , \mathbf{B} )\)をSpanning Bipartite Block Design (SBBD)と呼ぶ.

二部グラフの中の任意の2辺の選び方は，その共有点の状況により図1のように3通り考えられるため，それら3つに関する条件が(3,4,5)である.

さらに，\(\lambda_{21} = \lambda_{22}\) を満たすSBBDをGDD type といい，[5]では, GDD type SBBDの構成法や最適性について議論する. また，GDD type SBBDはGroup Divisible Designと呼ばれる組合せデザインと同値である.

Group Divisible Designの定義は以下の通りである.

[Group Divisible Design (GDD)の定義]