標準正規分布の幾何学的対称性
連続な確率変数の確率密度関数の積分形は、0から1までで評価できる累積分布関数です。では、累積分布関数を積分するとき、積分形の関数の一階の導関数は、累積確率として0から1までの傾きになります。つまり、直角三角形を用いた三平方の定理による評価が可能になります。そこで、標準正規分布の幾何学的対称性を応用しながら三平方の定理を用いてみると、新たな確率評価基準が思考できます。
欠陥データを利用したソフトウェアプロジェクト比較手法に関する研究
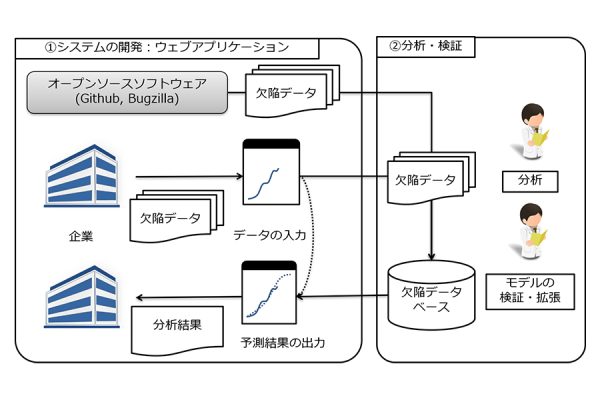
本研究では様々なドメインや開発スタイルに属するソフトウェア開発に対して有効なソフトウェア信頼性モデルを構築し活用方法を広く普及することでソフトウェア開発をより効果的で制御可能とすること目的とします。そのためには多くの企業の開発データの収集方法および普及方法としてウェブアプリケーションの開発が必要です。また企業の開発データのみならずオープンソースソフトウェアにおける開発データも対象とします。本研究を行うことで現在困難とされている開発スケジュールの定量的な決定に役立つと考えられます。
要素技術：
予期せぬ状況の把握（企業との共同研究）
テスト工程ごとに発見された欠陥を分類し、それぞれの工程で信頼性モデルを適用し、異変を検知します。実際のソフトウェア開発で発生する欠陥の情報を収集し、なぜ欠陥が増えたのか、個々の欠陥に関係性があるのかなど、開発の現場ではさまざまな分析を実施しています。しかし、欠陥が急激に増えることを予見することは簡単ではありません。そこで、ソフトウェア信頼性モデルを利用することで急激な欠陥数の変化を予見する方法を考え実証実験を行いました。
要素技術：
複数プロジェクトから基準となる信頼性モデル（企業との共同研究）
過去に開発した複数のプロジェクトの欠陥データを収集し、すべてのデータを用いてソフトウェア信頼性モデルを作成します。開発の進み具合を正確に判断することは難しいです。そこで、過去の開発した実績を利用して今の進み具合がどうか、判断できる基準となるモデルの構築をしました。開発の際に基準となるモデルと比較することで、開発中のプロジェクトの進み具合や問題が分かるようになります。基準を上回っていると「欠陥が多く出すぎているから今後ももっと出るのでは？」といった気づきや、基準を下回っていると「テストの内容が良くないかもしれない。テスト内容をチェックしなおそう」といった改善につなげることができます。
要素技術：
コードスメルの検出と修正
過去のプロジェクトに存在したコードスメル（問題が起きるかもしれないコード片）がどのようにして修正されているかについて調査しました。そもそも多くの方が利用されているソフトウェアに、どの程度コードスメルが存在するのか？という疑問から研究を始めました。そこでオープンソースソフトウェアを対象に、Apacheという組織が開発している5つのプロジェクトに対してコードスメルをSonarQubeというツールを利用して分析しました。分析結果として一つのプロジェクトを例に出すとおよそ6000個のコードスメルが見つかりました。このように普段利用しているソフトウェアにもコードスメルが存在し、問題につながる可能性が十分に存在しています。そこで、このコードスメルを検出し修正する方法を検討するために、どういったコードスメルが修正されているかを調査し、修正しやすいコードスメルを見つけることで自動でコードスメルを修正できるかどうか検討しています。
論文
「Detection of Unexpected Situations by Applying Software Reliability Growth Models to Test Phases」(2015)『2015 IEEE International Symposium on Software Reliability Engineering Workshops (ISSREW)』p.2-5.
「Case Study: Project Management Using Cross Project Software Reliability Growth Model Considering System Scale」(2016)『2016 IEEE International Symposium on Software Reliability Engineering Workshops (ISSREW)』p.41-44.
「オープンソースソフトウェアにおけるCode Smellと対応するリファクタリングの特徴に関する調査」(2021)『ソフトウェアエンジニアリングシンポジウム2021』
研究シーズ・教員に対しての問合せや相談事項はこちら
技術相談申込フォーム