組合せ構造の機械学習への応用
2017年より, 組合せ構造の深層学習への応用を研究している. 本シーズでは, 二部グラフをブロックとしてもつ組合せ構造spanning bipartite block designの構成法について紹介する.
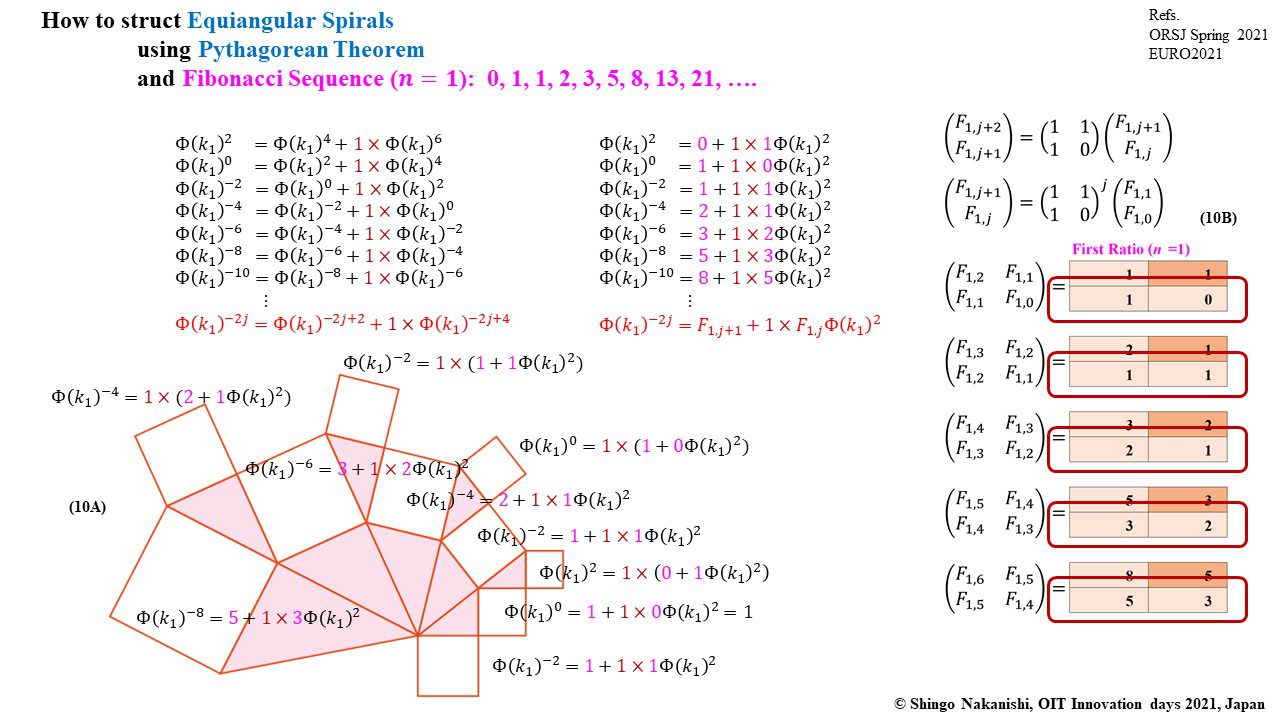
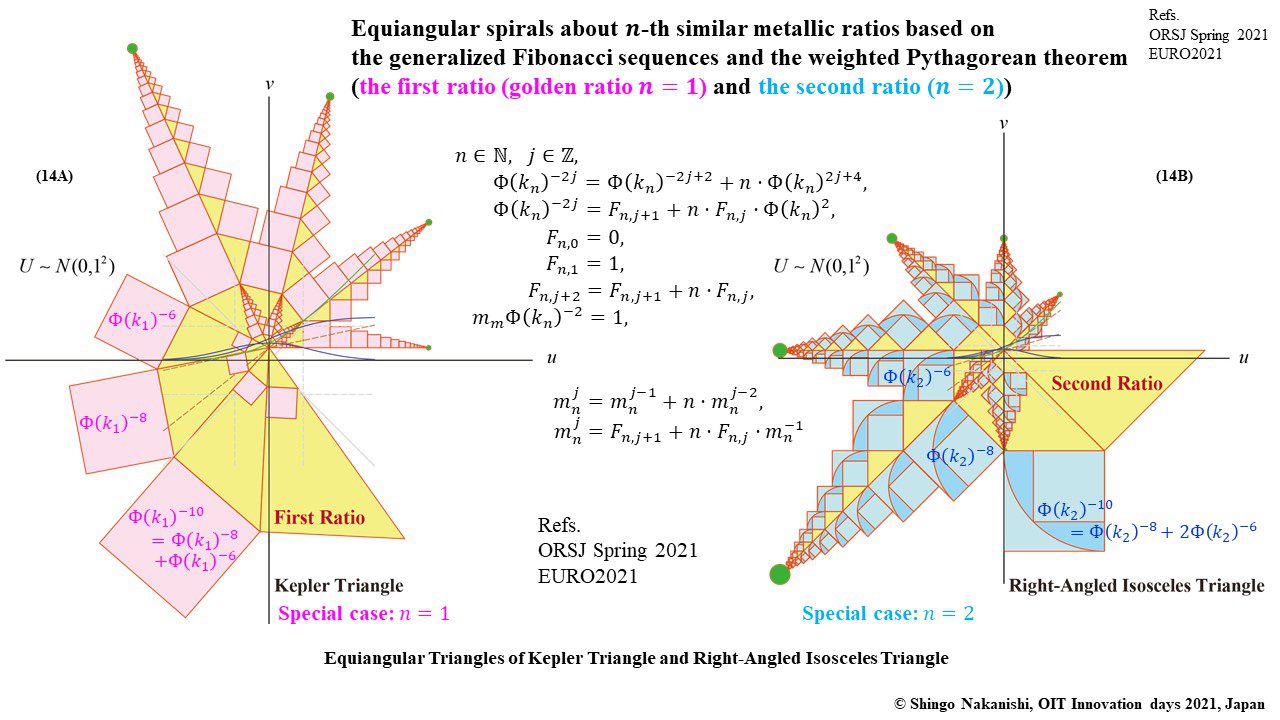
セカンダリーの貴金属比が奏でる数理情報デザイン 等角螺旋を目指したケプラー三角形とピタゴラスの定理と一般化されたフィボナッチ数列の協奏
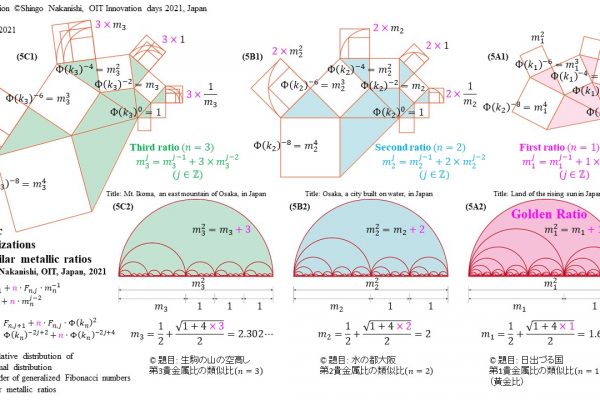
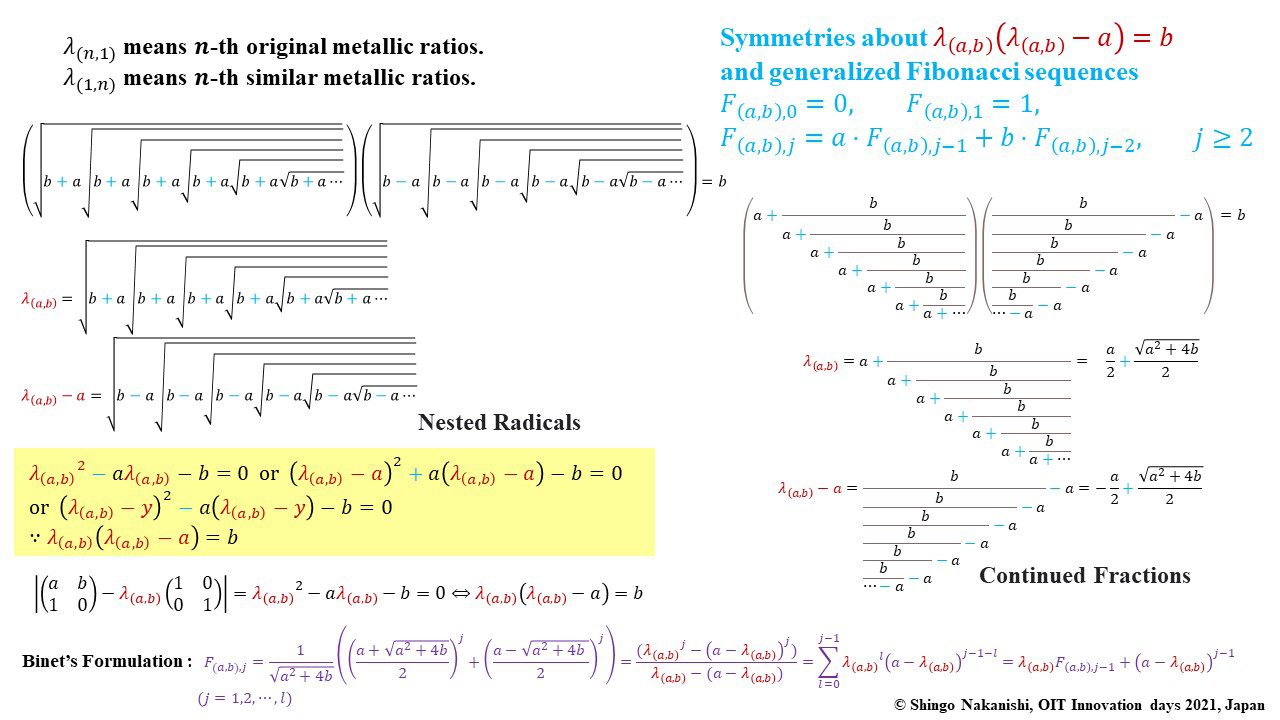
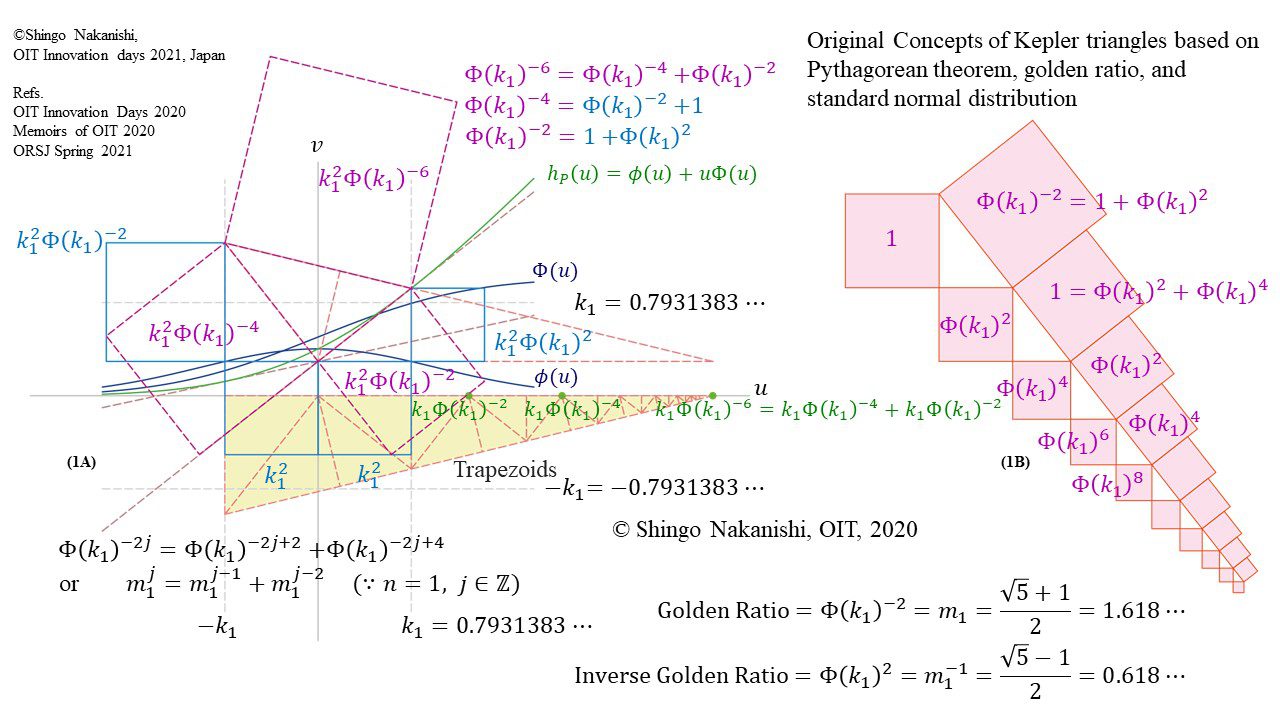
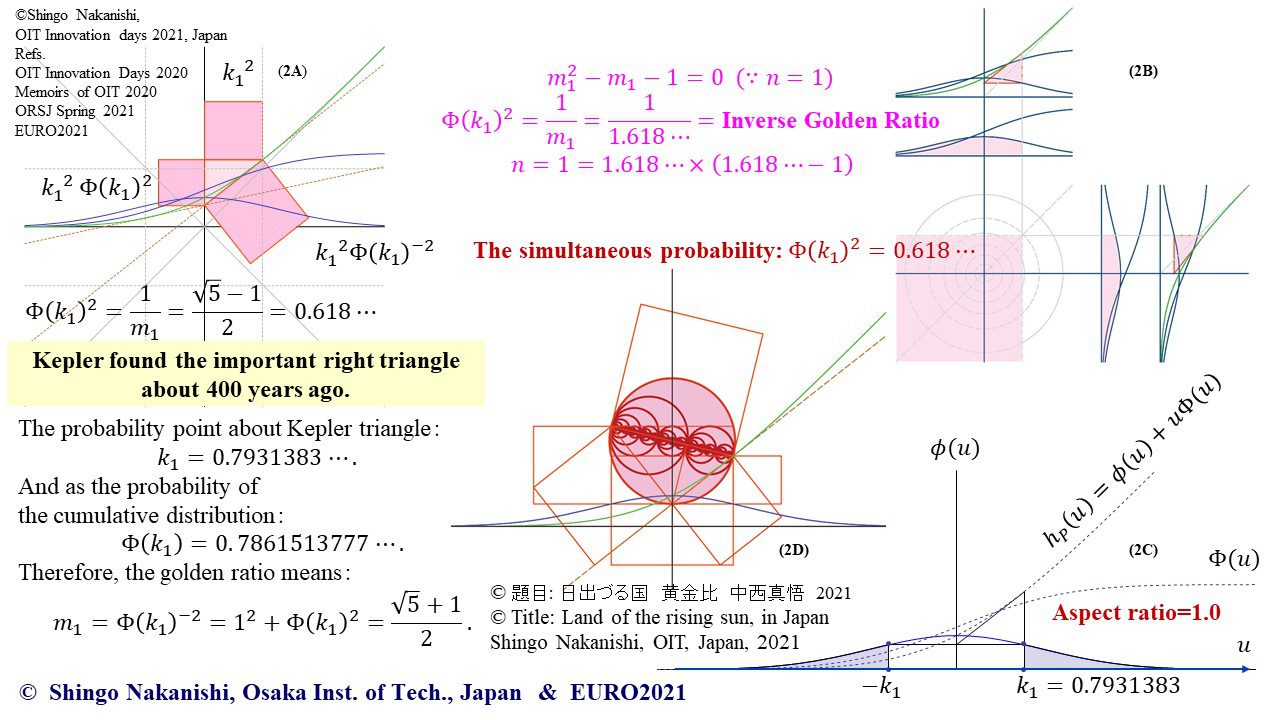
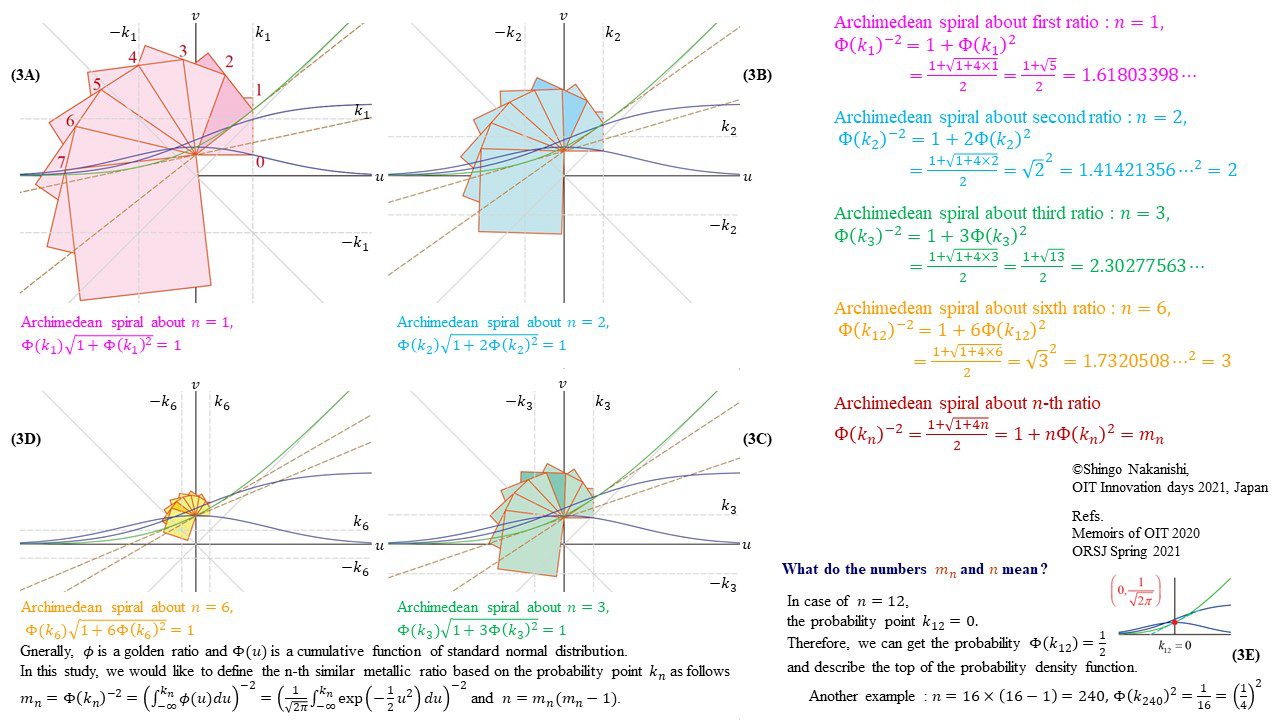
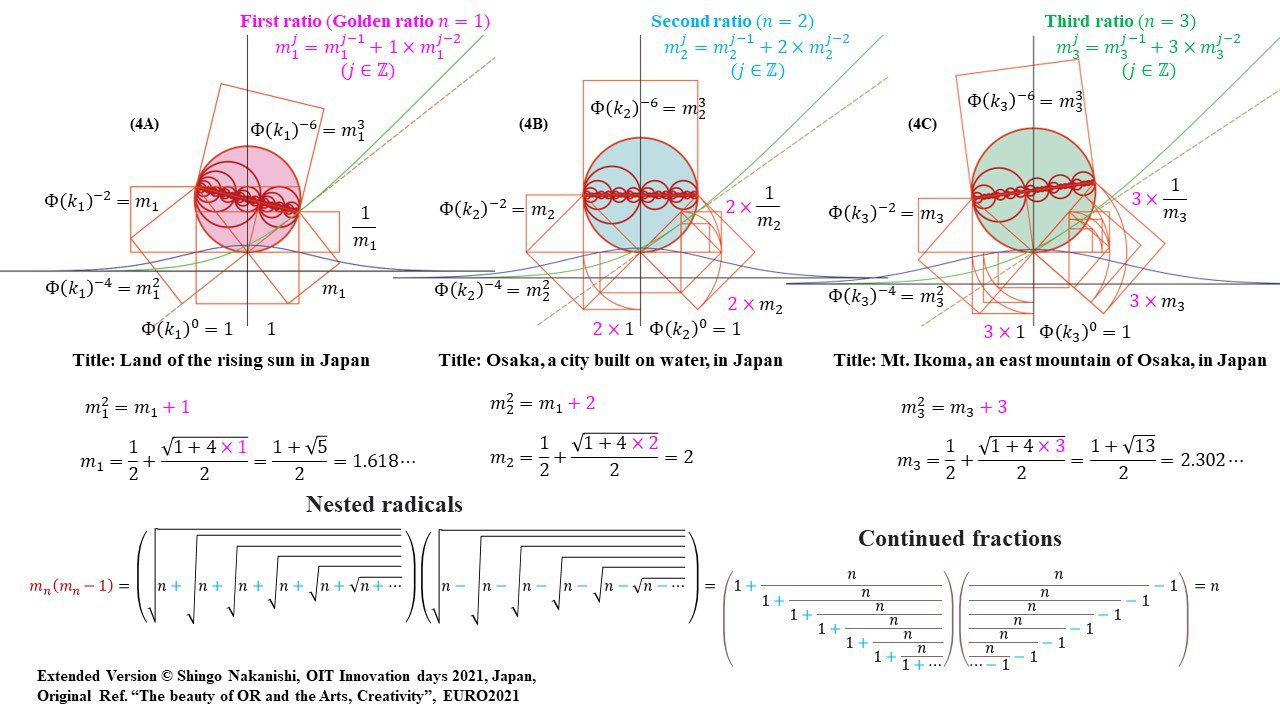
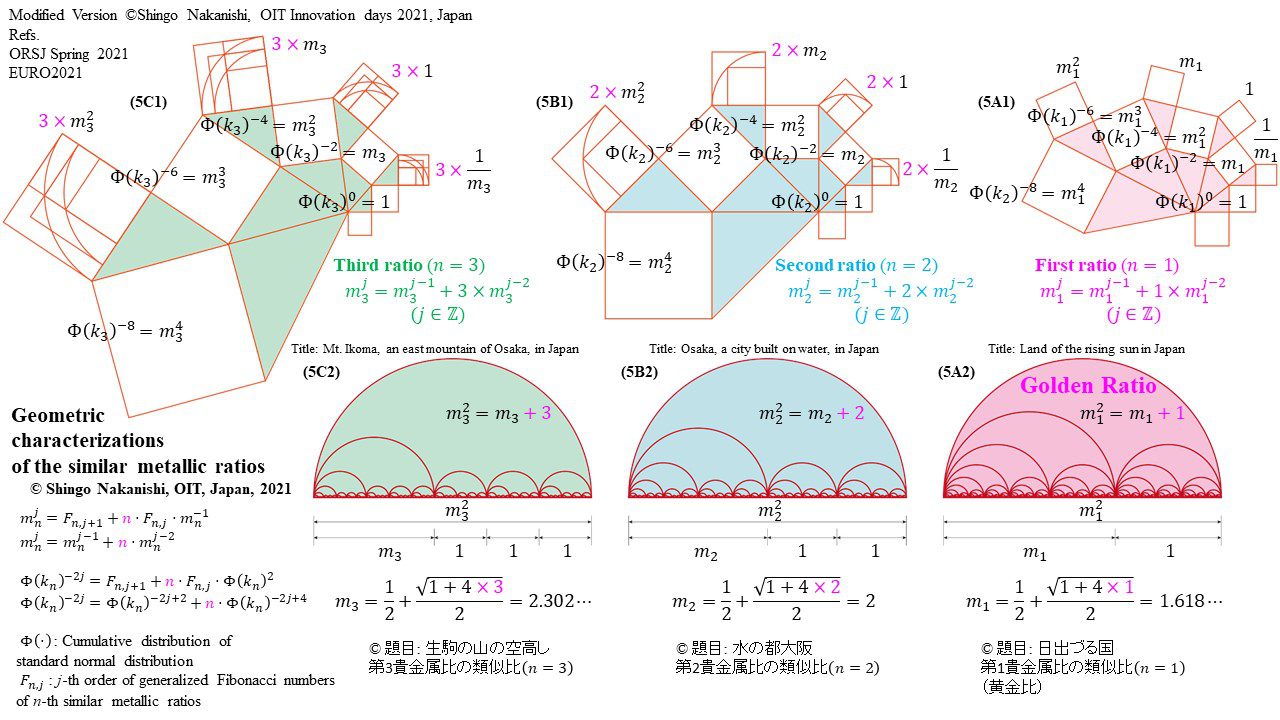
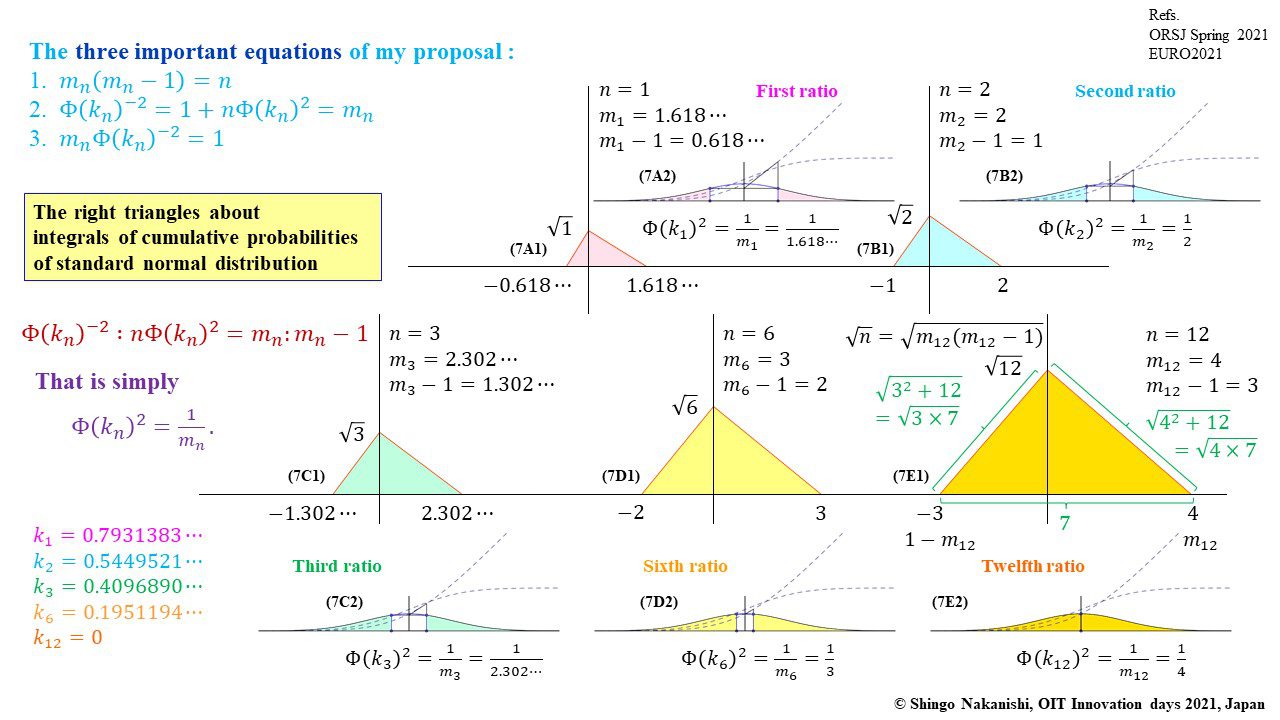
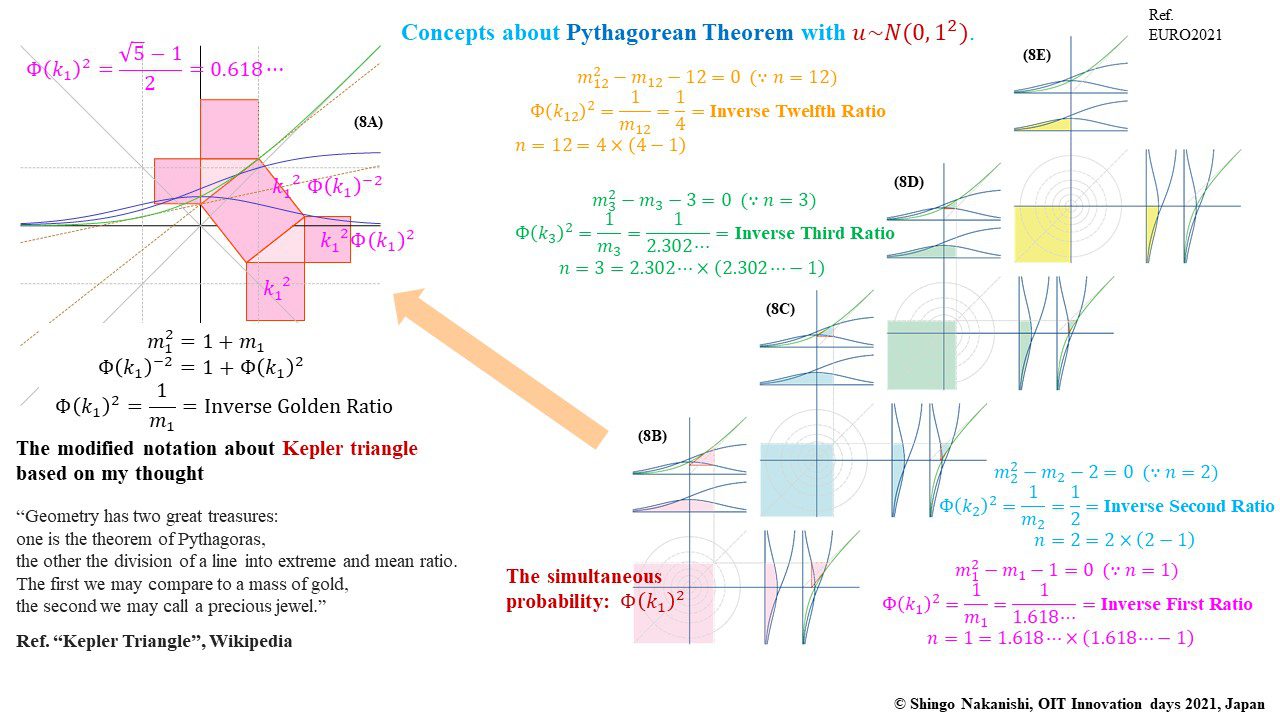
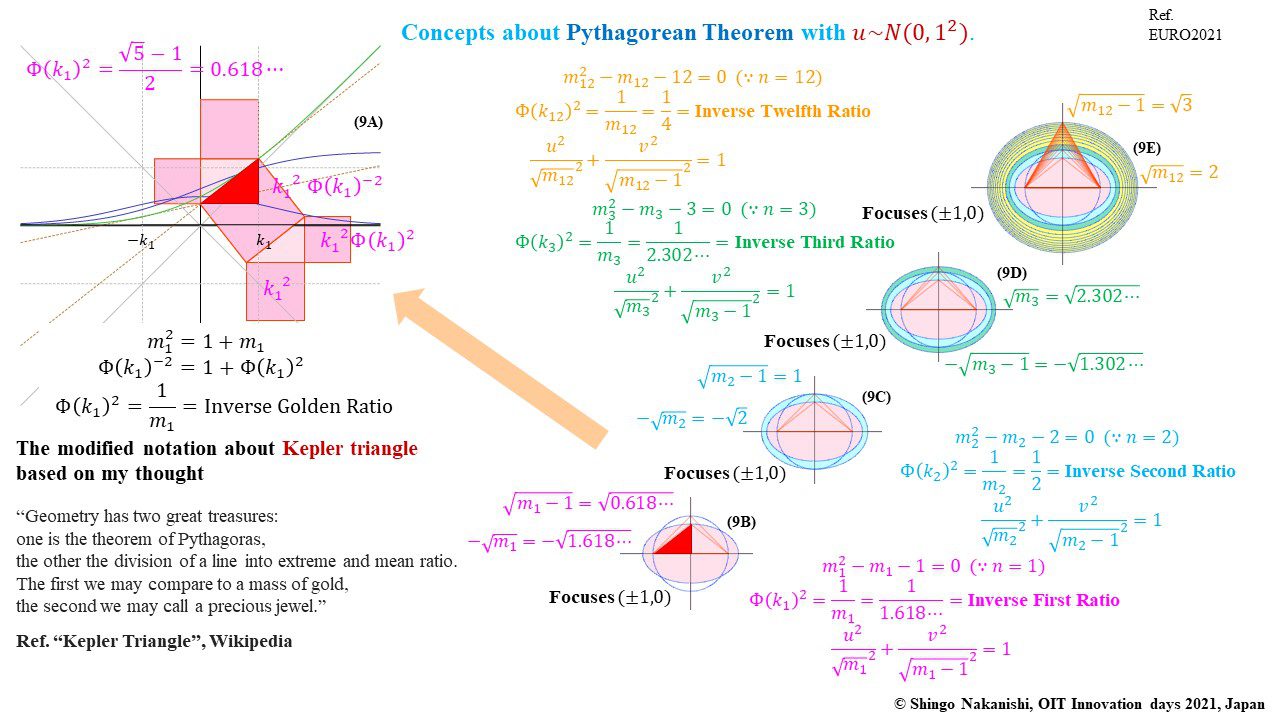
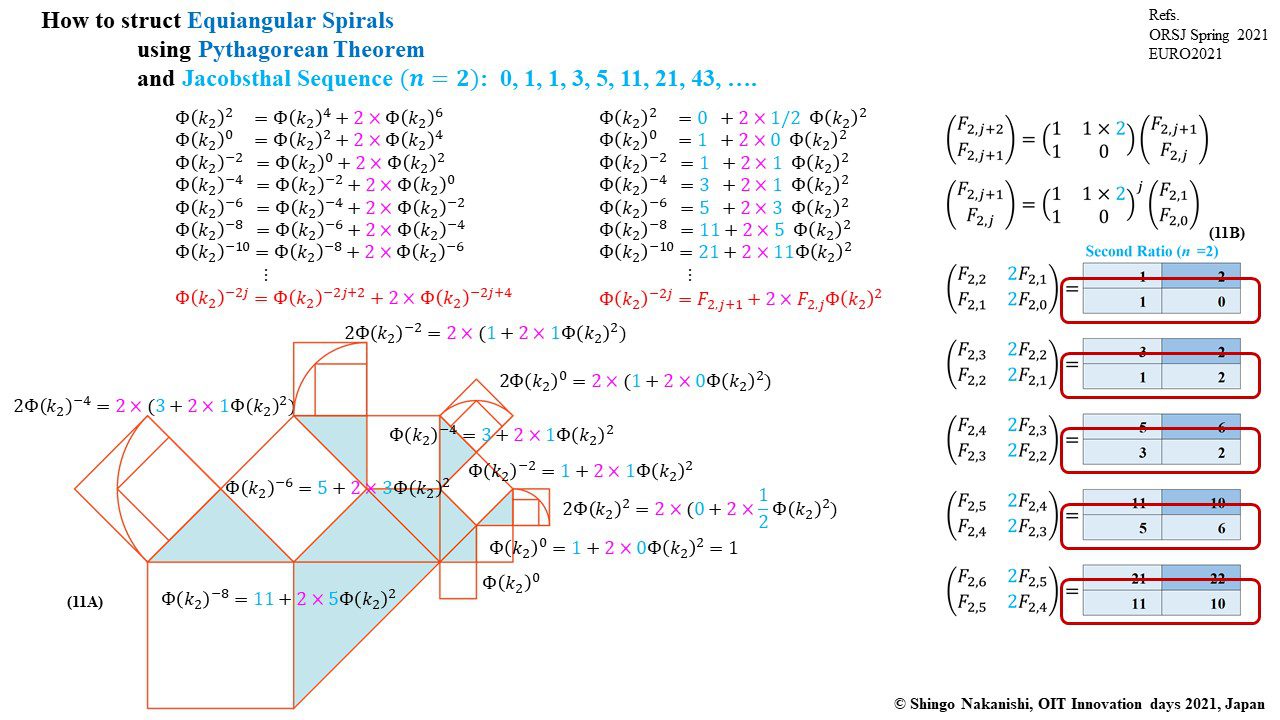
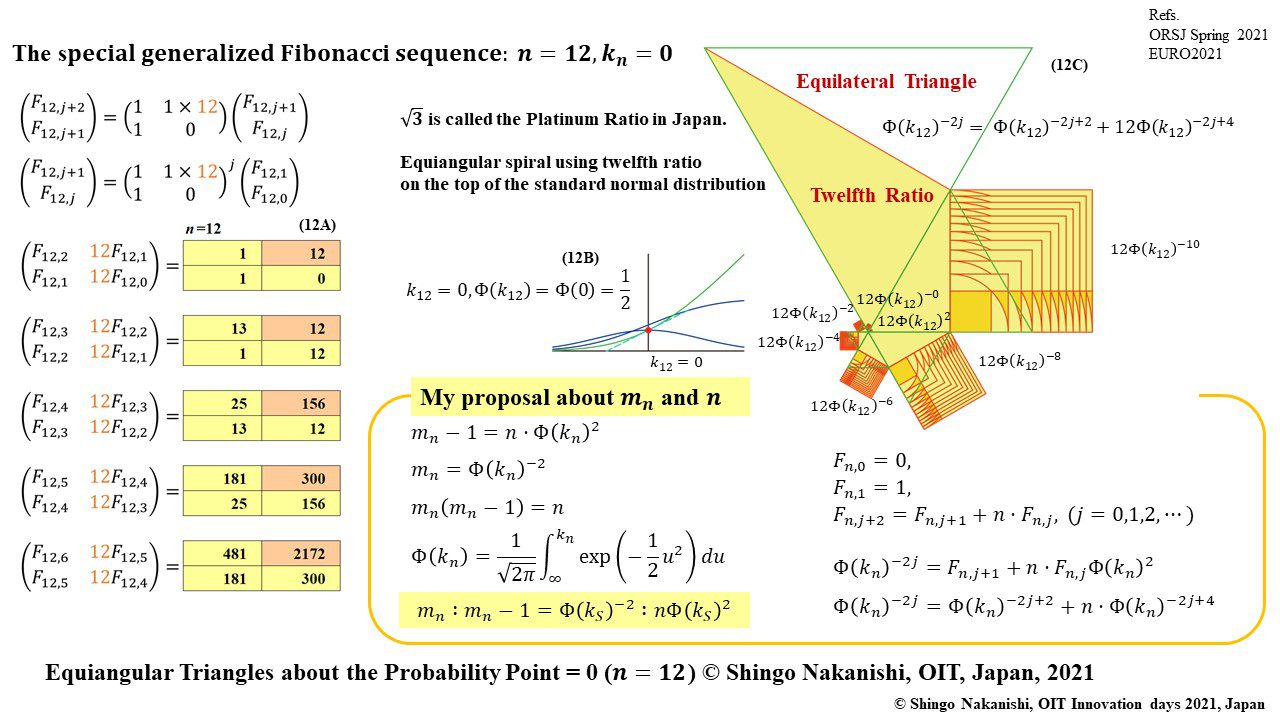
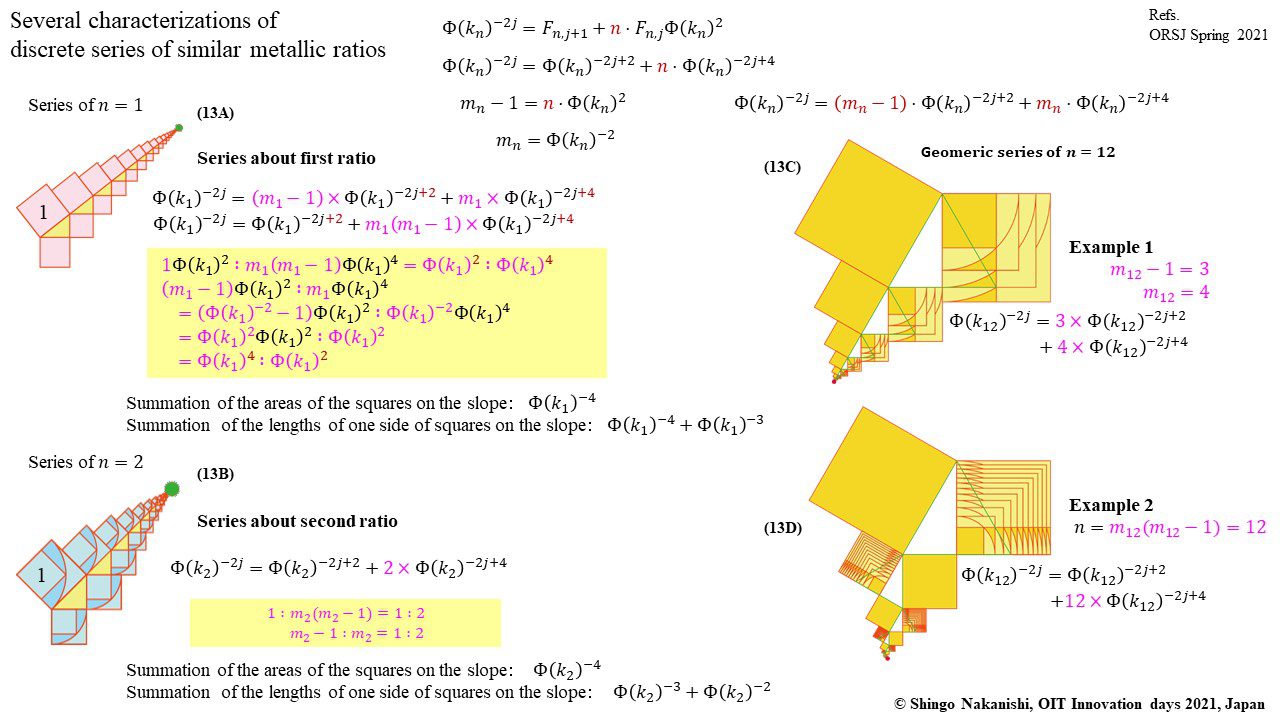
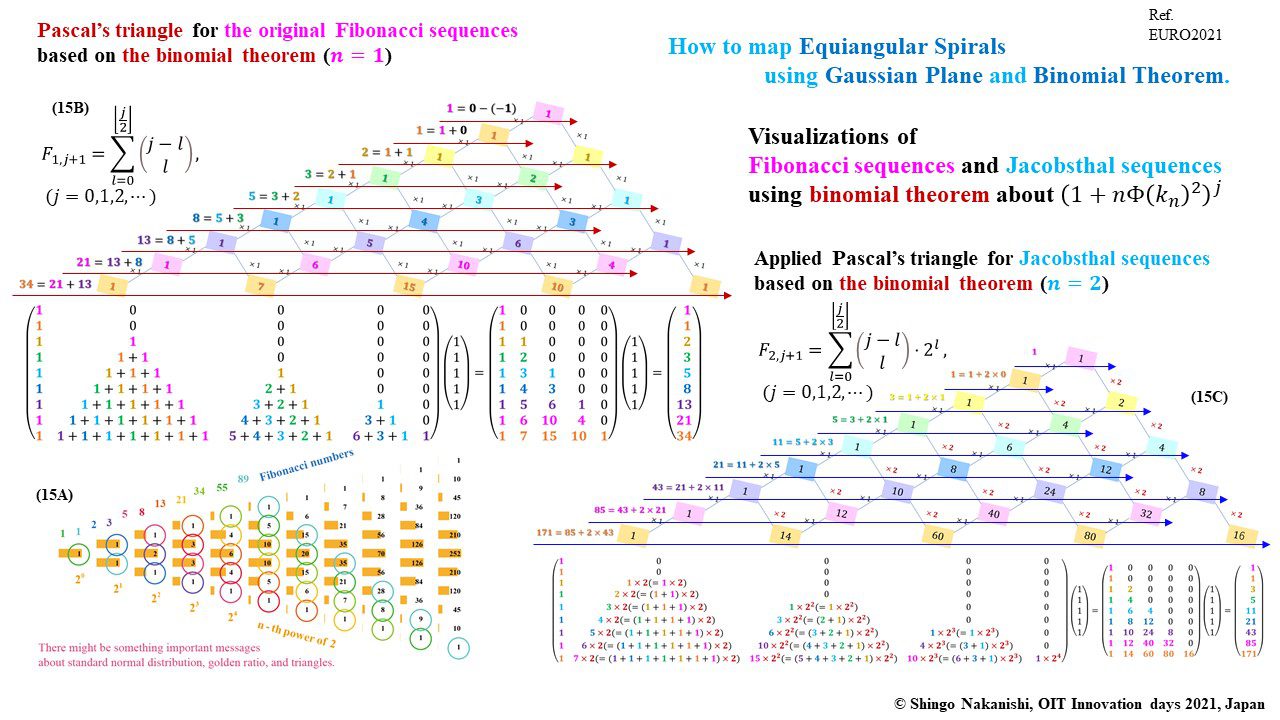
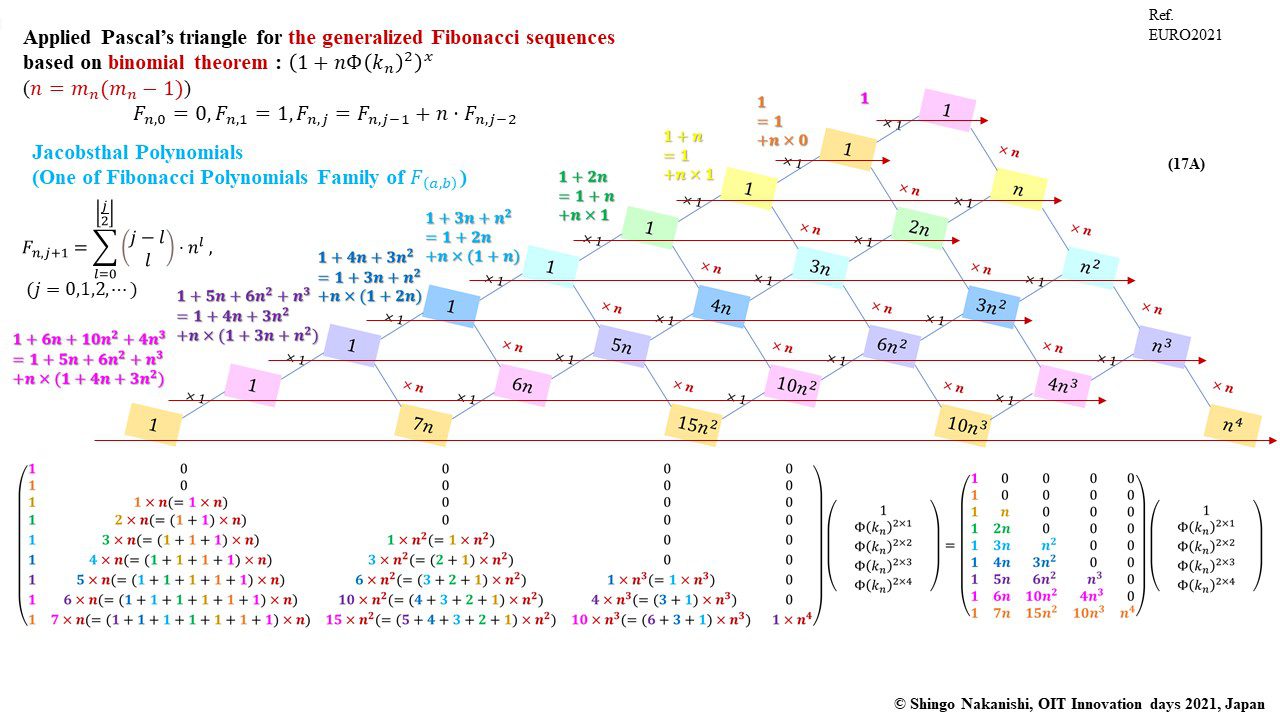
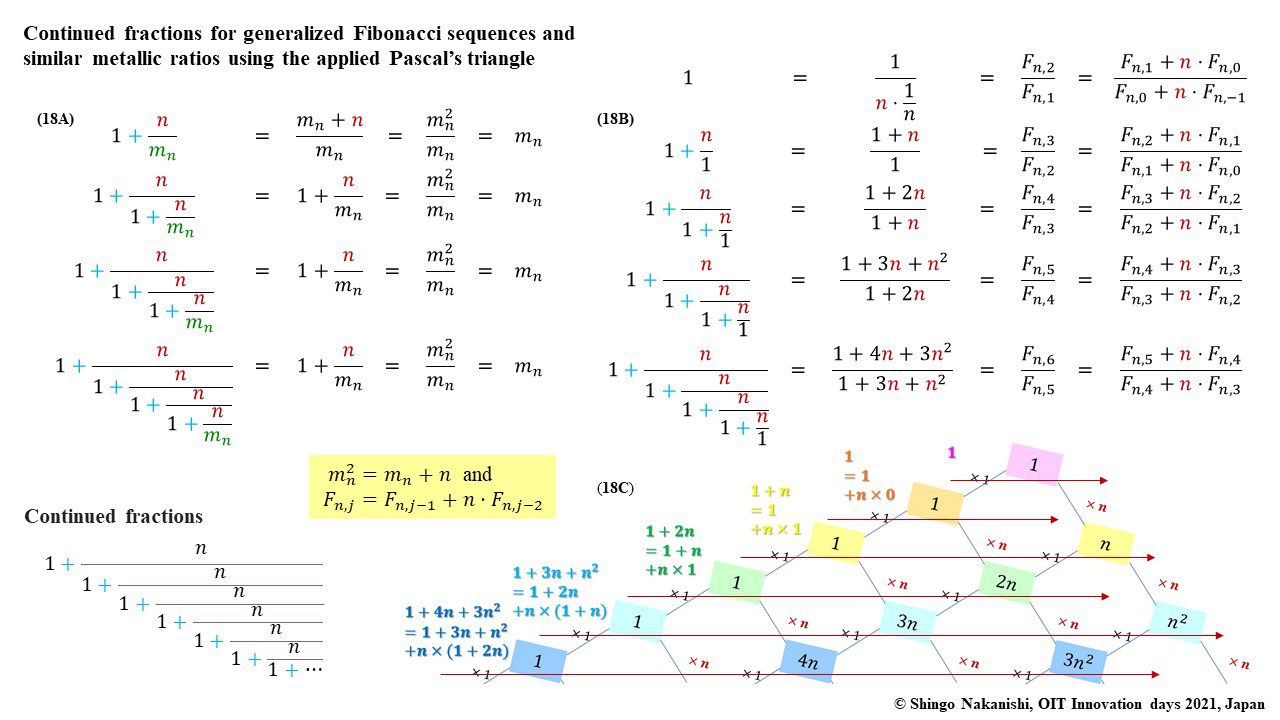
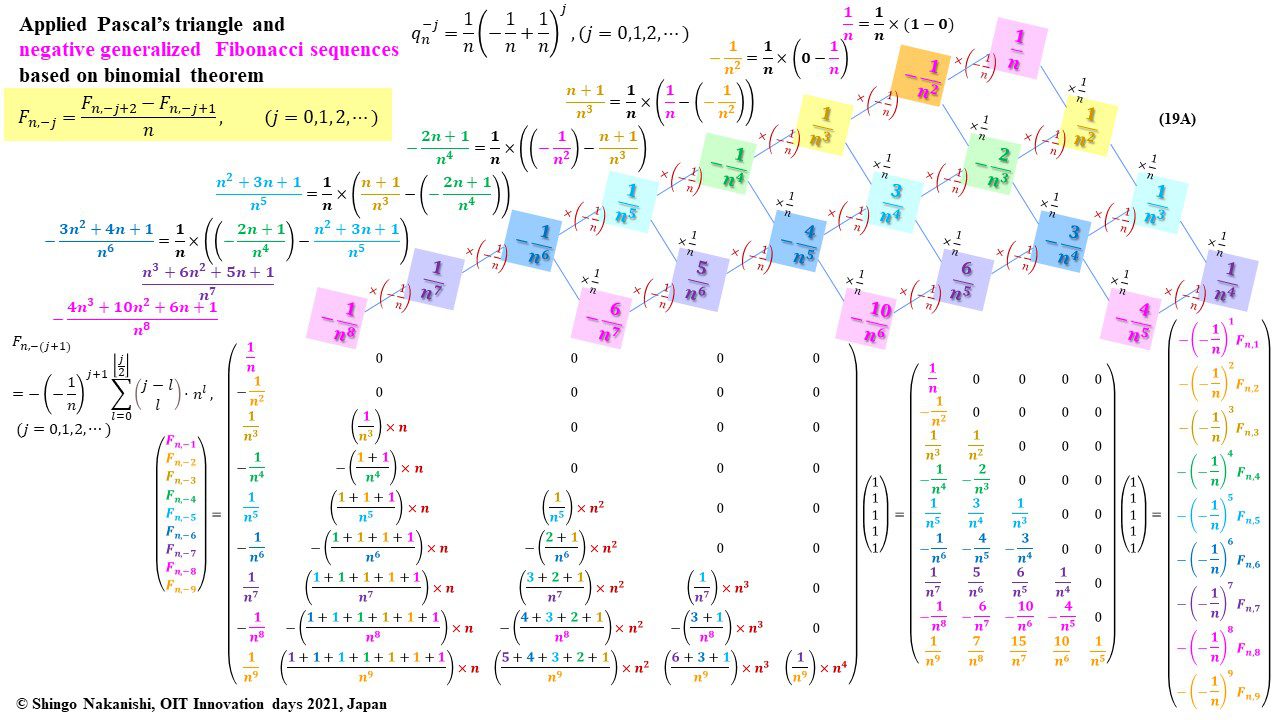
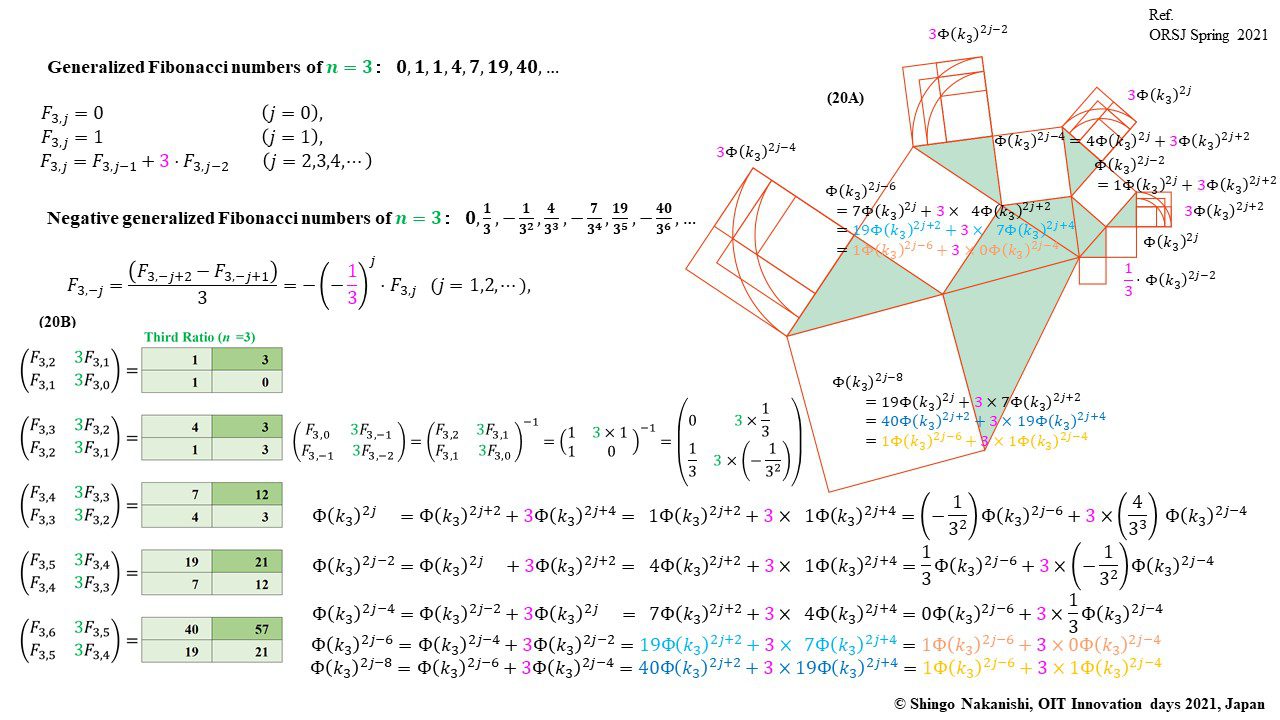
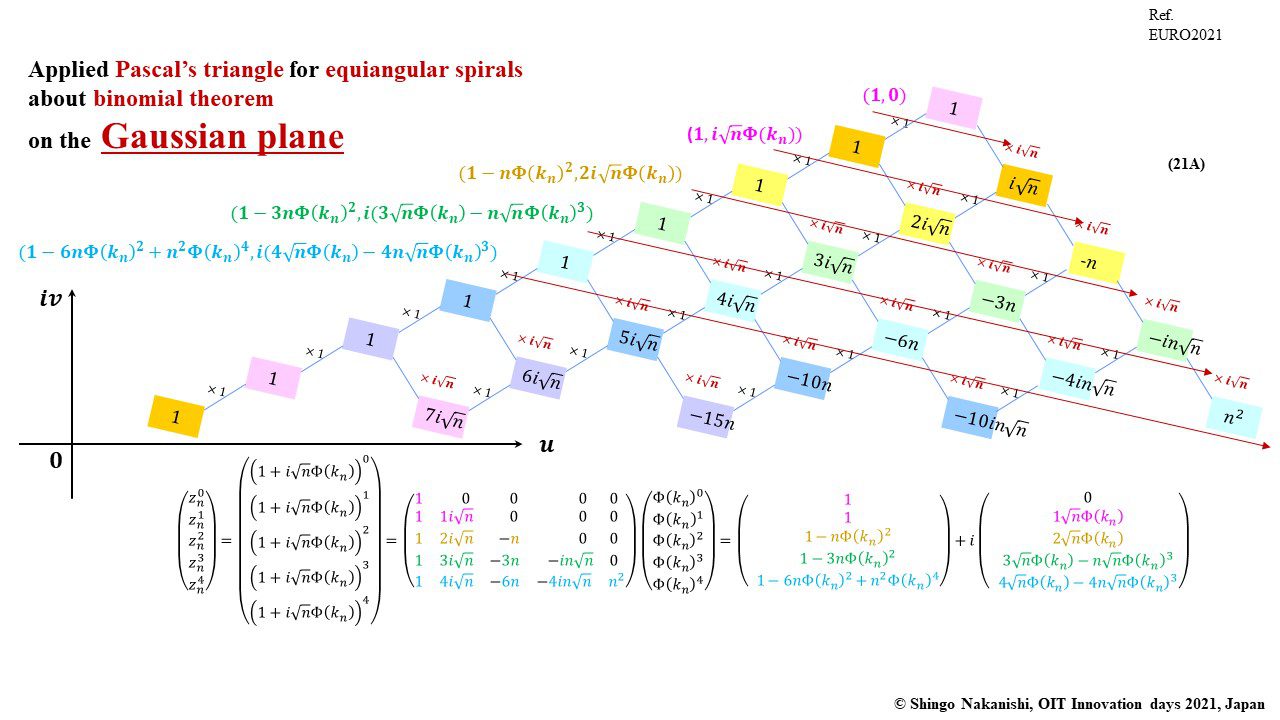
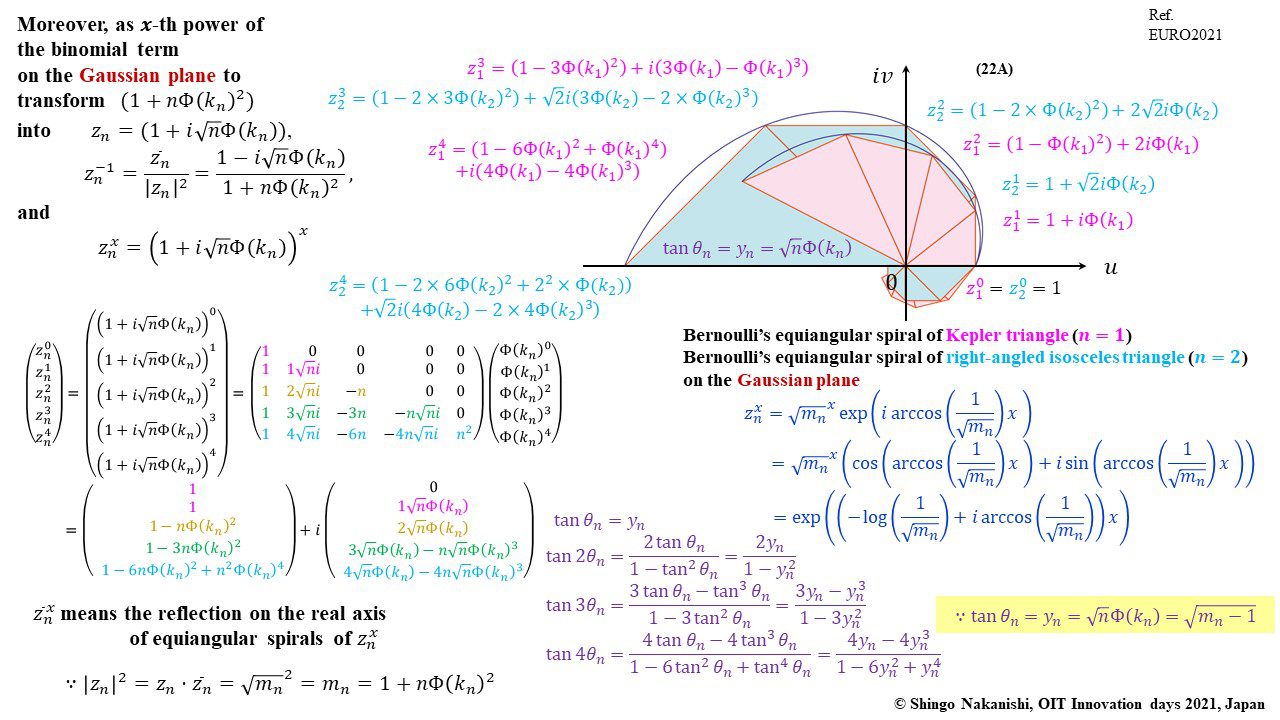
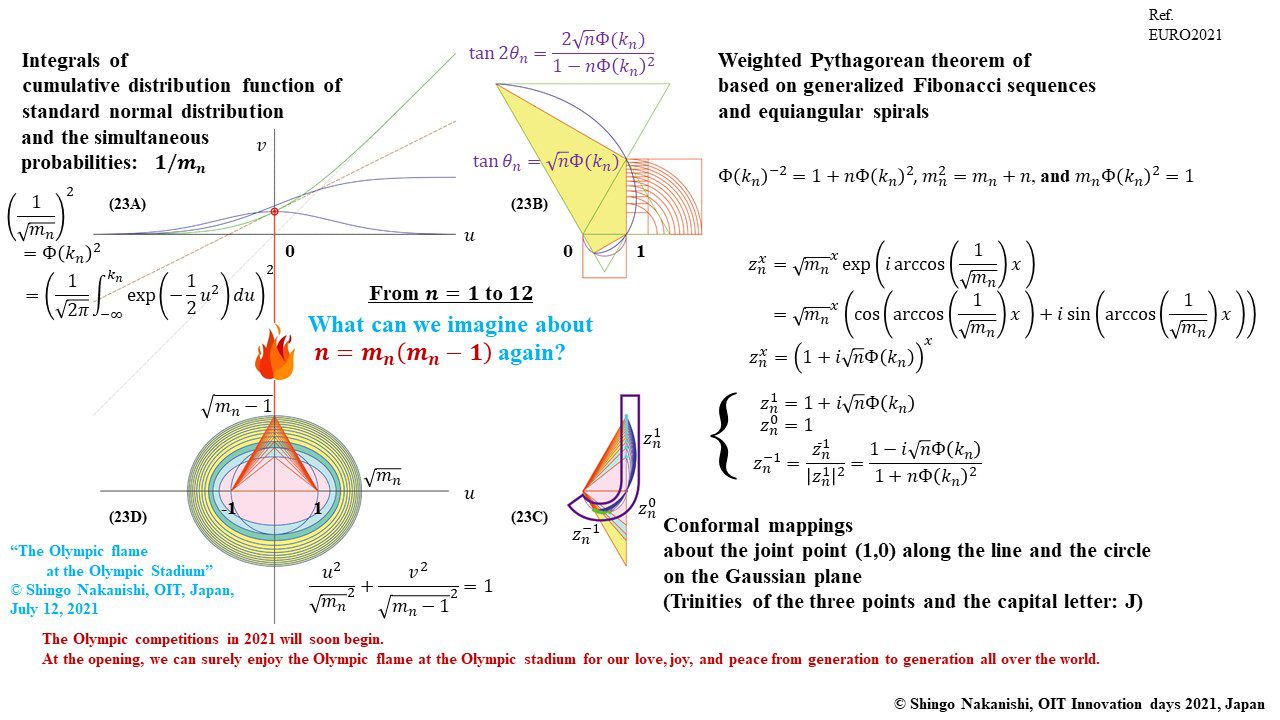
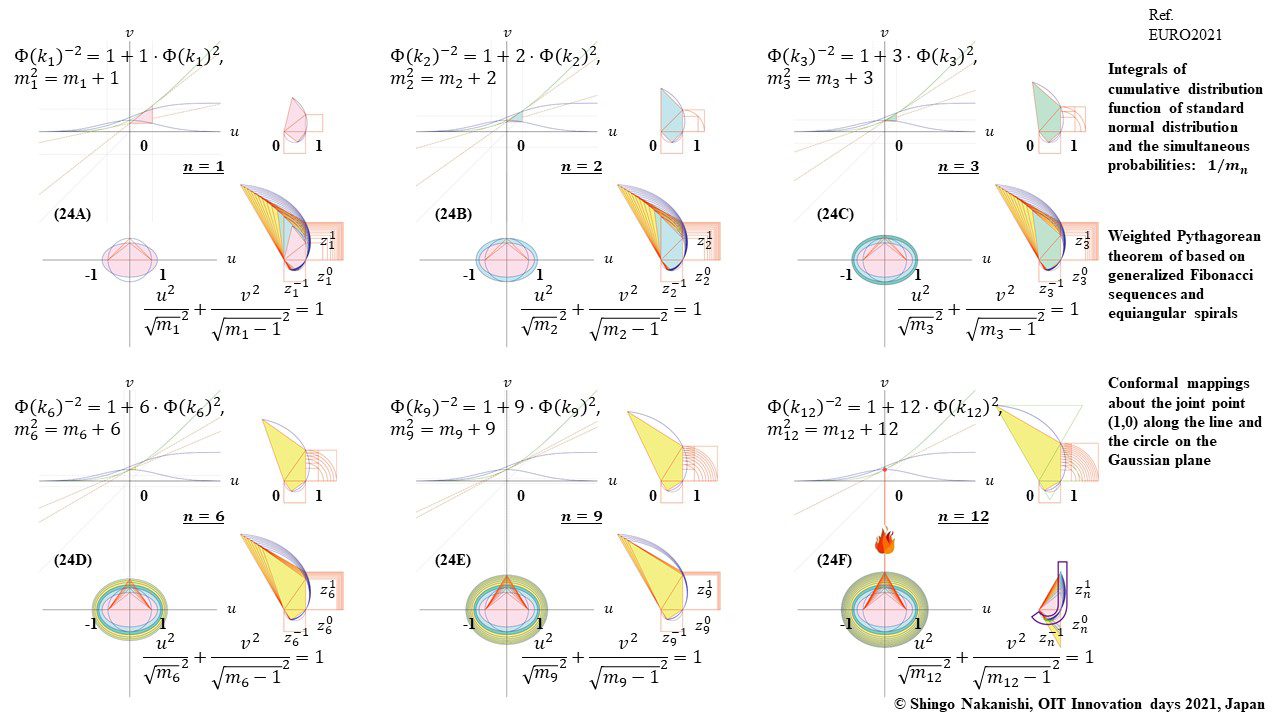
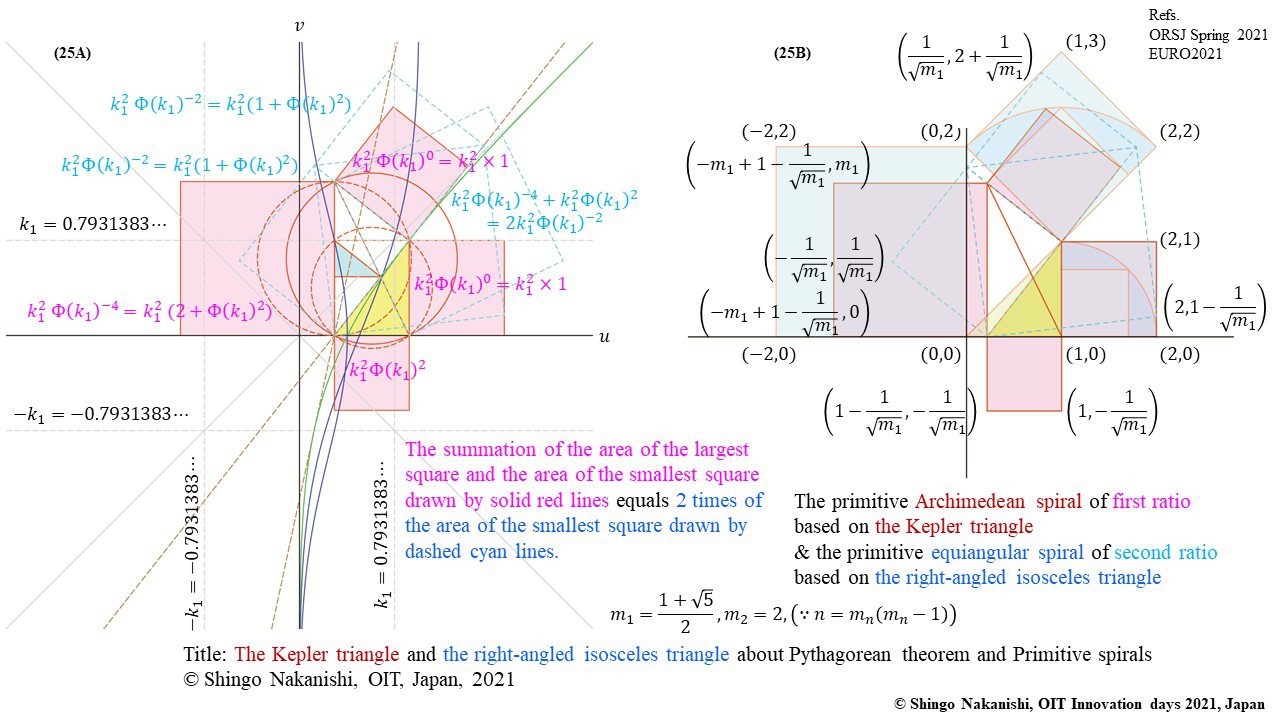
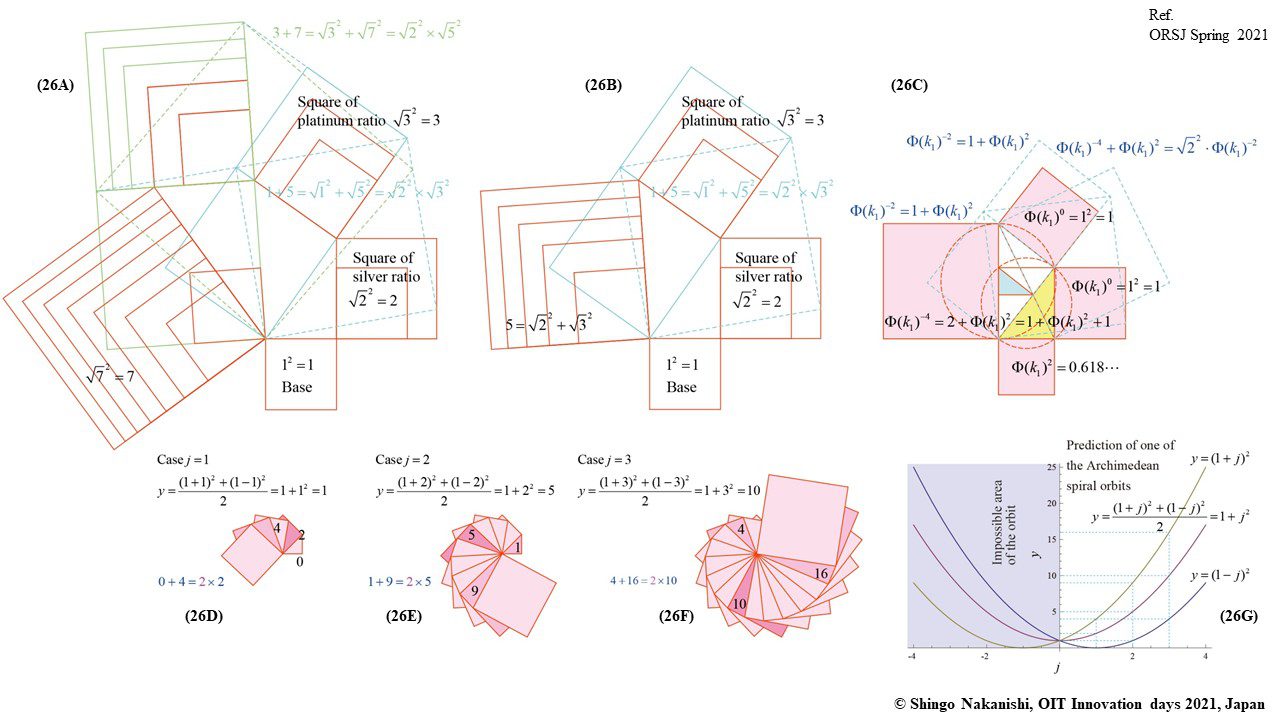
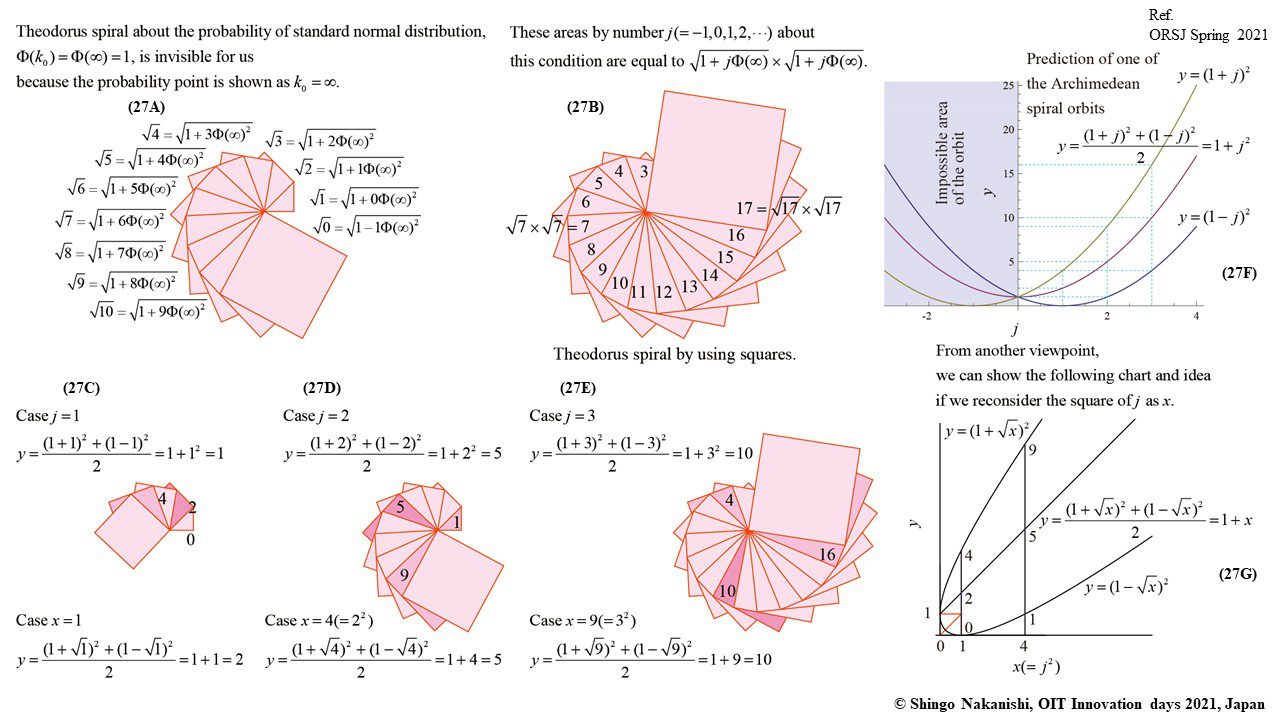
セカンダリーの貴金属比を類似比と読み替えてお楽しみください．黄金比とピタゴラスの定理を魅了させるケプラー三角形に、一般化されたフィボナッチ数列を応用した新たな貴金属比の類似比の魅力を提案しました。発表後に定義式には第2類似比がカッパー比、第3類似比がニッケル比と1990年代後半に命名されていたことがわかったのですが、命名者も際立った数学的・芸術的魅力は言及しませんでした。一方で、従来の貴金属比の第4貴金属比にもカッパー比、第5貴金属比にもニッケル比が記載されることがあり、名称の由来や情報とその信憑性に確信を持てませんでした。したがって、発表時のコンセプトの通りに従来の第2貴金属比である白銀比、第3貴金属比である青銅比を基準に対比しながら今回の発表を公開して、ご閲覧いただく皆様のご意見を聴くことにしました。科学・技術ならびに芸術の世界に役立つ発展に繋がれば嬉しいです。ところで、白銀比に必要な直角二等辺三角形と、ペル数列の代わりにヤコブスタール数列を活用した貴金属比の類似比には、従来の貴金属比とは導出こそ異なるけれども、とても美しい数理と芸術の可能性が隠されていました。貴金属比の類似比の幾何学的特徴を調べながら、有名な数学者の功績を加えて調和させていくと、その美に魅せられます。下記は、提案から1年間の成果のギャラリーです。ご堪能ください。
貴金属比と貴金属比の類似比の呼称の説を右の図に掲載します。二通りございます。de Spinadelが類似比を1990年代後半に見つけたようです。既にこのときに黄金比と白銀比はデザインの世界で、市民権を得ていたので、第3貴金属比に青銅比、第2類似比にカッパー比、第3類似比にニッケル比と命名したようです。これより古い文献に、英語版でも日本語版でも青銅比や白金比は今のところ見つかっていません。一方で、第4貴金属比にカッパー比、第5貴金属比にニッケル比を定義する文献も見つかります。どちらが本当かに関心はあるのですがわかりません。そこで、下記の作品を制作するときに、第2類似比は白銀比に、第3類似比は青銅比の特徴をいかに保つ類似比となるかに焦点を当てて今回は製作しました。したがって、動画サイトのビデオでは、発表当時のまま、白銀比と青銅比の名称を活用して公開しています。
まずは、貴金属比と貴金属比の類似比の魅力ですが、多重根号と連分数による表記が可能なことです。a=n, b=1の場合が従来の貴金属比に相当し、a=1, b=nの場合が貴金属比の類似比に相当します。
このとき、1を引いて実現する黄金比の逆数に相当する多重根号と連分数は収束しないので使えないのではと尋ねられるかもしれません。無限に実証することはもちろん無理かもしれませんが、Excelを使用して初項にとても小さな数εを加えると再帰する値が黄金比の逆数に収束していきます。したがって、1+εを大体1であるとみなせば実用に耐えられます。
ところで、黄金比とピタゴラスの定理を考えるとき、日本では馴染みのないケプラー三角形が主役となります。これに加えて、ピタゴラスの定理とフィボナッチ数列が大活躍します。ちなみに本研究の提案までは、ケプラー三角形の日本語版Wikipediaは存在しませんでした。ケプラー三角形に興味を持たれた方は、本研究の動画を動画サイトでお楽しみください。
この研究は、標準正規分布の累積分布関数を傾きとして用いたときにヒントを得ました。特に、左の図ではケプラー三角形の底辺を原点からの確率点までの距離として正規化するときに、三角形の高さが傾きと一致するため、ピタゴラスの定理が活かされます。そして、二次元標準正規分布の同時確率を黄金比の逆数として定義するときに、その魅力は発揮されます。
はじめは、右の図のようにアルキメデスの代数螺旋の特徴について調べていました。下の図2枚は、その後に得られた新たな貴金属比の類似比の概念図です。
芸術的にも面白い図が描けたので、記念して
- 黄金比には「日いづる国」
- 白銀比に対応した第2類似比には「水の都大阪」
- 青銅比に対応した第3類似比には「生駒の山の空高し」
と命名しました。陽の光、水、野山の大切さを感じていただけると嬉しいです。
上記でも説明しましたが、左上の図の貴金属比の類似比には連分数と無限多重根号による表記により、貴金属比の類似比の序数との美しい関係が見つかりました。また、この解は2次方程式を解くことでも得られるし、特性方程式を用いて固有値として求めることもできます。そして、その固有値から幾何平均の考え方により個性ある直角三角形を表現することができました。下の図2枚はそのことを図示しています。その結果、この関係図から序数ｎは、貴金属比の類似比と（類似比ー１）の積で示せることがわかりました。右上の図には、類似比の幾何学的意味を単純に表した概念図です。このときに再帰する考え方が役立ちます。
貴金属比の類似比の定義は上記の概念図で行ったので、右の図では、その数値の逆数に合わせて二次元標準正規分布の同時確率を視覚化しています。ｎ＝１２では、確率点が図の中心である原点になることが、後ほど重要となります。すなわち、確率である２分の１を二乗して４分の１を図示しています。これにより、貴金属比の類似比が４のため、ｎ＝４×（４－１）＝１２となります。
次に、ケプラーの別の功績でもある楕円を活用して、右上の図の関係を右の図のように楕円を用いて視覚化してみます。ｎ＝１では、ケプラー三角形を活用し、同様にｎ＝２では、直角二等辺三角形を活用し、ｎ＝１２では、正三角形を活用します。すなわち、二つの正規化された楕円の焦点と一番上の楕円の軌道の点を用いて直角三角形を描くことができます。この関係はピタゴラスの定理の活用が重要な意味を持つことを暗示しています。
それでは、真の黄金比や白銀比の等角螺旋（対数螺旋）と呼ばれる螺旋構造を解明します。まず、黄金比はケプラー三角形とピタゴラスの定理とフィボナッチ数列とを用いて左下の図のように描けます。ルート２を意味する白銀比はその派生型である従来のペル数列の代わりにヤコブスタール数列を用いるときに、ピタゴラスの定理と直角二等辺三角形を用いて同様に描くことができます。これまでの黄金比の螺旋の提案とは異なり、この発想は独自のものです。
ところで、ｎ＝１２のときには、本来は確率点が０のために、標準正規分布の頂上に1点だけが表示され、螺旋構造は描けません。もし、描けるとしたら、どのように描くことができるのだろうかとイメージしてください。その答えが左下の図です。すなわち、ｎ＝６が本来のルート３を意味する白金比の序数に相当する類似比なのですが、実際に白金比に対応した等角螺旋を描くときには、ｎ＝１２の類似比のほうが幾何学的には都合が良いことがわかりました。また、いくつかの連なりの幾何学的特徴も左下に図示しました。
連なりの部品も併せて、これらの特徴を兼ね備えた黄金比と白銀比（第2類似比）のフラクタルを目指したデザインに関する等角螺旋図は左の図のように描くことができました。従来の黄金比や白銀比に対応する等角螺旋のイメージとはかなり異なる図が描けていることがわかります。
一方で、フィボナッチ数列と相性の良い数学の道具としてパスカルの三角形も考えることができます。そこで、左下の上図には、従来からの関係図として有名な図を示し、それと同様に、白銀比をヤコブスタール数列を用いて表せるとしたらどのように描けるかを左下の下図に示します。また、右下の図のように、重みづけをした桁ずらし算を応用して考えた場合には、二項定理との関連も数理的に見通しが良くなることがわかりました。
このことを応用するならば、一般化されたフィボナッチ数列についても二項定理を活用して図示することができます。したがって、一般化されたフィボナッチ数列と連分数の関係も図示でき、その解明に大変役立ちました。左下の図はヤコブスタール多項式との関係を視覚化しています。
同様に、負の一般化フィボナッチ数列も左下の図のように図示できます。この特徴を右下の図のように青銅比（第3類似比）の場合に適用して確認してみました。
続いて、ガウス平面上（複素数平面上）で等角螺旋の特徴を調べるために、同じ考え方で左下の図のように二項定理を活用します。その結果をもとに、この特徴を黄金比に対応するケプラー三角形と白銀比（第2類似比）に対応する直角二等辺三角形を同時に重ねた等角螺旋として右下の図のように比較しています。この螺旋の特徴は、等角螺旋の連続版についてもド・モアブルの定理を活用しながら考察できます。また、二項定理の実部と虚部の関係は正接の加法定理と同じ効果を得ることができます。このことはかなり昔から等角を描く方法として知られていたようです。
以上の特徴をｎ＝１２のときにまとめて図示したものが右の図です。別頁に掲載している動画ではこの図を活用して五輪の開会式のイメージの予想しながら開催の十数日前に発表しました。
その動画のコマを分割して、黄金比（第1類似比）、白銀比（第2類似比）、青銅比（第3類似比）と変化していく様子をまとめて表したものが右の図です。すなわち、四つの特徴である①標準正規分布上での直角三角形、②貴金属比の類似比に関するピタゴラスの定理、③等角螺旋のガウス平面上での視覚化、④同じ焦点を持つ貴金属比の類似比に関連した楕円が変化していく様子をそれぞれ視覚化しています。
ここまでの数理的特徴を追求するときに、ケプラー三角形の存在はとても大きく、黄金比（ケプラー三角形）と白銀比（直角二等辺三角形）の関係について多角的に調べる機会を得ることができました。左の図はそのときの黄金比と白銀比の組み合わせの図の成果です。
その他のおまけとして、代数螺旋軌道の構造に次の三つの図が示す関係も見つかりました。
すなわち、ある螺旋上の点を起点として代数螺旋軌道の前後では距離が同じとなる点での二つの正方形の面積の和が、起点に位置するその中間の正方形を二つ加算した和に等しいことが導出できました。現在は貴金属比のとの関連を精査中です。
また、おまけ②として固有値の関係を調べていた時には、今回提案した貴金属比の類似比とその序数には、類似比が整数である場合に限定しなければ、ピタゴラスの定理を用いて説明ができる特徴があることを示せました。
今回の研究成果の特徴をもとに黄金比（第1類似比）と白銀比（第2類似比）をもう一度ペアにして描きます。いかがでしたか。ご興味いただけた場合、あるいはもっと知りたい場合は、別頁に掲載している動画をご視聴ください。ここまでご覧いただきありがとうございました。
以上より，この研究は，上の図のように，黄金比とピタゴラスの定理がケプラー三角形を構成し，それがフィボナッチ数列により等角螺旋を構成しました．そして，ガウス平面上で下記のようにオイラーの公式に黄金比が重なり等角螺旋の連続版を説明できました．
そして，このセカンダリーの数式の第一項の係数を眺めるとフィボナッチ数列は２に，ヤコブスタール数列は３になります．この意味が，他のシーズでも説明したように，正三角形と正六角形の螺旋図に融合しました．とても嬉しい結果と結びついて感動しました．感謝です．再度，有難うございました．
論文
「ピタゴラスの定理と標準正規分布に基づく螺旋および等角図の幾何学的考察 ― 三角形と正方形や貴金属比の類似比によるアプローチ ―」(2021)『大阪工業大学紀要』65(2)p.103-127.
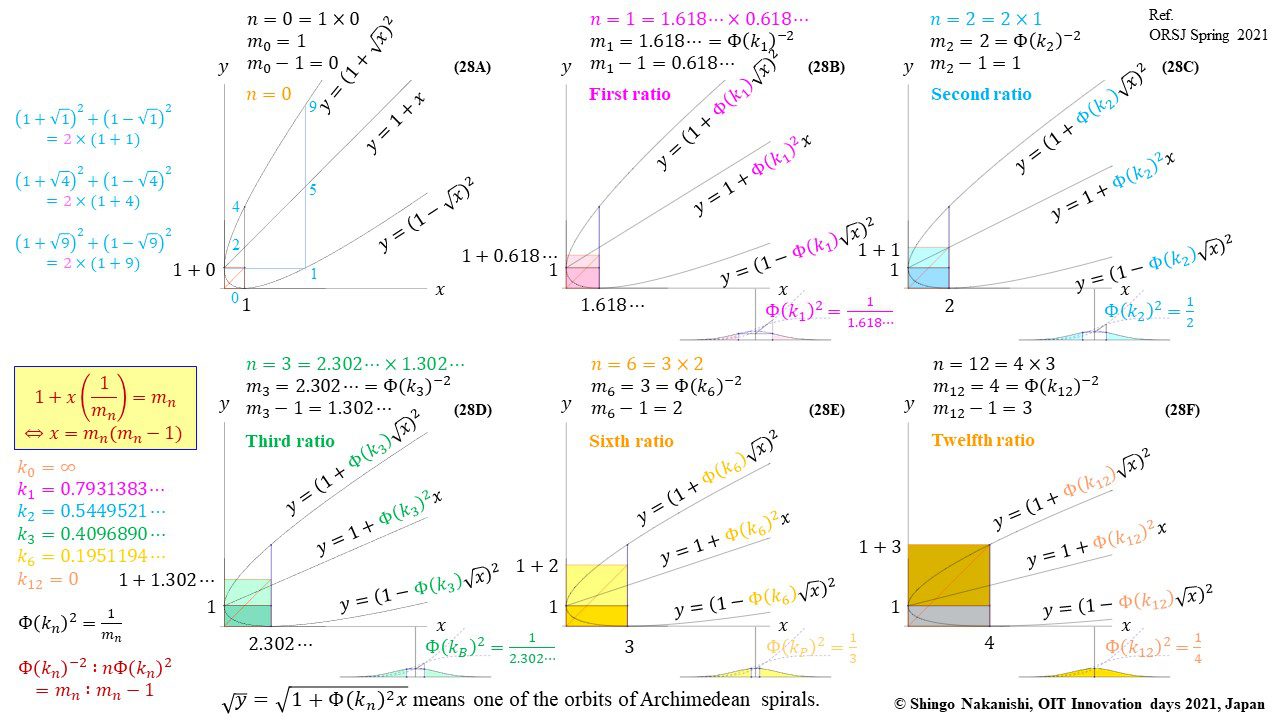
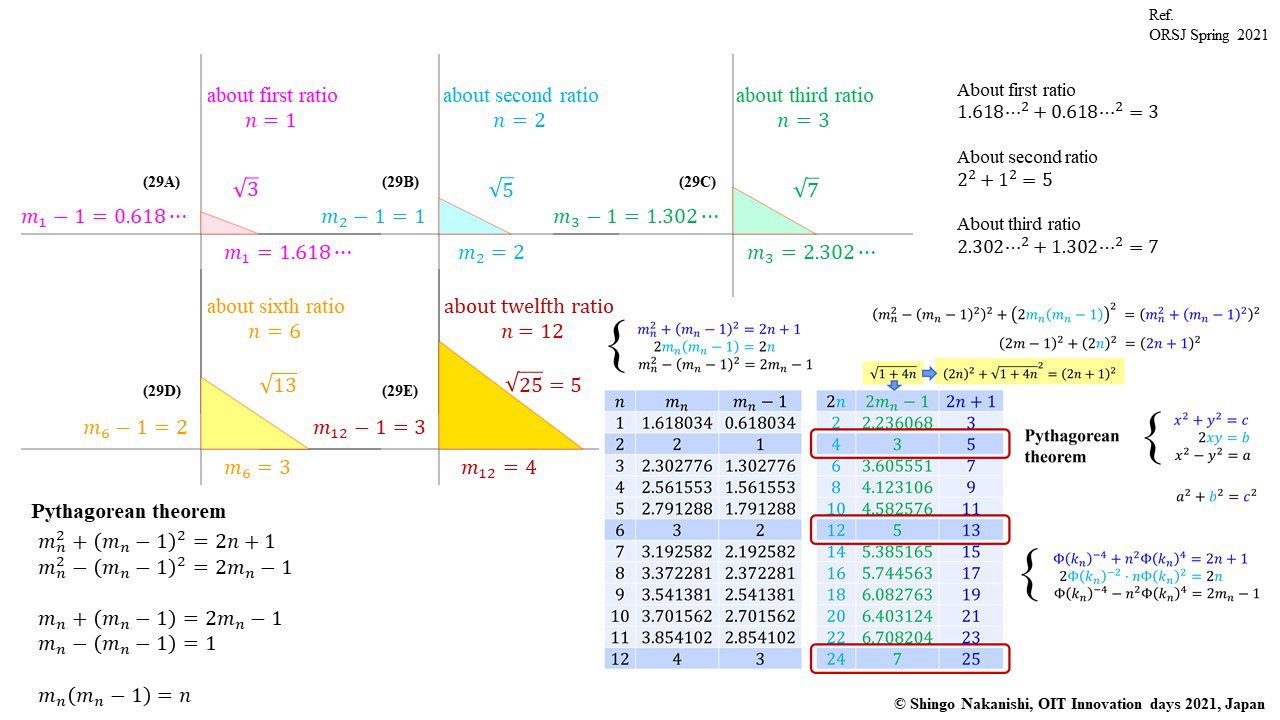
「標準正規分布の累積分布関数を傾きとする黄金比や貴金属比の類似比 (その1) ケプラー三角形,ピタゴラスの定理,平方および代数螺旋の再考」(2021)『日本オペレーションズ・リサーチ学会春季研究発表会アブストラクト集 』2-E-10p.1-2.
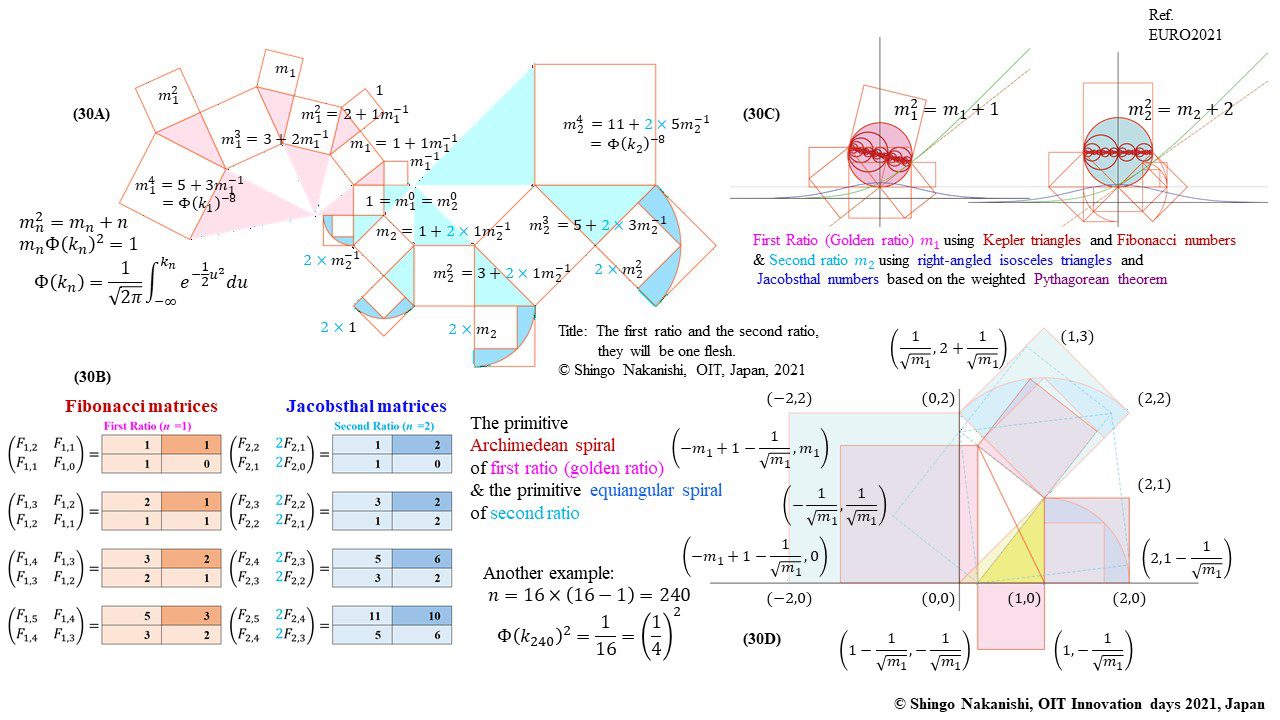
「標準正規分布の累積分布関数を傾きとする黄金比や貴金属比の類似比 (その2) フィボナッチ数列の拡張とフラクタルを目指した等角螺旋デザイン」(2021)『日本オペレーションズ・リサーチ学会春季研究発表会アブストラクト集 』2-E-11p.1-2.
研究シーズ・教員に対しての問合せや相談事項はこちら
技術相談申込フォーム