標準正規分布の幾何学的対称性
連続な確率変数の確率密度関数の積分形は、0から1までで評価できる累積分布関数です。では、累積分布関数を積分するとき、積分形の関数の一階の導関数は、累積確率として0から1までの傾きになります。つまり、直角三角形を用いた三平方の定理による評価が可能になります。そこで、標準正規分布の幾何学的対称性を応用しながら三平方の定理を用いてみると、新たな確率評価基準が思考できます。
交互方向乗数法を用いた分散スケジューリング
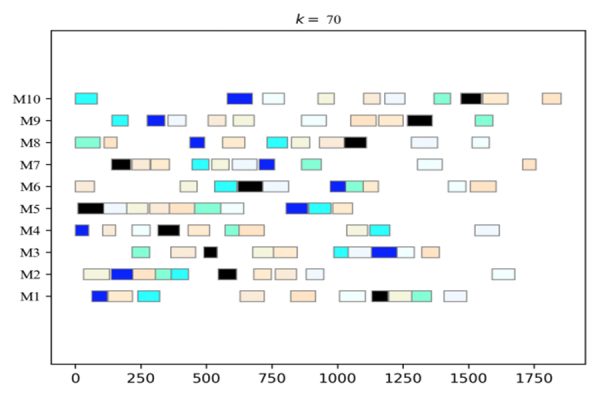
スケジューリング問題をマルチエージェント系での合意問題として捉えることによって，交互方向乗数法を用いた分散スケジューリングによって解く方法を開発した。
概要
マルチエージェント系において，エージェントによる最適化とエージェント間の通信を繰り返す事によって，最適化を行う手法を分散最適化という。
本研究では，スケジューリング問題を分散最適化問題として捉え，交互方向乗数法（ADMM: alternating direction method of multipliers）を用いた解法を提案した。
右図の実行例では，10機械，10ジョブのスケジューリング問題を解いている。機械毎にエージェントが存在し，それぞれのスケジュール（図では横一列がそのエージェントが作成するスケジュールを表す）を作成している。繰り返し回数（図中のkの値）が増えるにしたがって，実行可能なスケジュールが形成されている。
論文
「分散スケジューリング問題に対する合意に基づく解法」(2021)『システム制御情報学会論文誌』34(2)p.58-67.
研究シーズ・教員に対しての問合せや相談事項はこちら
技術相談申込フォーム