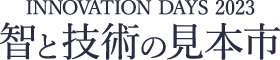液体の粉体化技術に基づく機能性材料の創出
コロイド次元に存在する高分子粒子は、接着・粘着、塗料分野においてフィルム形態にして広く利用されている。近年、高分子粒子の粒子径、粒子径分布、表面化学、形状のコントロール技術の発展の恩恵を受け、大きい比表面積、分散状態における適度な運動性を活かした粒子形態のままでの利用にも関心が集まり、学術、工業両分野において精力的に研究が進められている。さらに、コロイド次元にある高分子粒子は、粒子間力、界面自由エネルギー、媒体の流れを駆動力とする自己組織化、すなわち自律的方法によって省エネルギー型の機能性材料の創出を可能にし、現行の重力支配下におけるエネルギー消費型の材料創出、すなわち他律的方法を見直す機会を我々に与えてくれる。 発表者は、界面自由エネルギーを駆動力とする粒子の自律的な界面吸着現象に注目し、高分子粒子の気液分散体の安定化剤としての利用を提案している。これまでに、粒子径、単分散性、形状、表面化学を精密にデザインした機能性高分子粒子を使用し、高分子化学、界面コロイド化学を学術基盤として、高分子粒子によるアーマードバブル、リキッドマーブル(LM)、ドライリキッド等のソフト分散体の安定化、構造評価および安定性制御に関する基礎研究を推進している。粒子の素材として高分子材料を利用することで、無機材料では導入が困難である、多様性に富む刺激応答性、低温での変形能、成型性、フィルム形成能の導入が可能になり、ソフト分散体を基盤とする新規機能性材料の開発につながると考えている。本発表では、気中液滴型気液ソフト分散体であるLMについて、発表者らが取り組んできた研究について紹介させていただく。